Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-12T08:10:47.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Convective effects and the role of quadrupole sources for aerofoil aeroacoustics

Published online by Cambridge University Press:  10 August 2012

William R. Wolf ,
João Luiz F. Azevedo  and
Sanjiva K. Lele
William R. Wolf*
Affiliation:
Department of Aeronautics & Astronautics, Stanford University, Stanford, CA 94305, USA Institute of Aeronautics and Space, São José dos Campos, SP 12201-970, Brazil
João Luiz F. Azevedo
Affiliation:
Institute of Aeronautics and Space, São José dos Campos, SP 12201-970, Brazil
Sanjiva K. Lele
Affiliation:
Department of Aeronautics & Astronautics, Stanford University, Stanford, CA 94305, USA Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: willwolf@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The present investigation of aerofoil self-noise generation and propagation concerns the effects of mean flow and quadrupole sources on the broadband noise that arises from the interaction of turbulent boundary layers with the aerofoil trailing edge and the tonal noise that arises from vortex shedding generated by laminar boundary layers and trailing-edge bluntness. Compressible large-eddy simulations (LES) are conducted for a NACA0012 aerofoil with rounded trailing edge for four flow configurations with different angles of incidence, boundary layer tripping configurations and free-stream Mach numbers. The Reynolds number based on the aerofoil chord is fixed at . 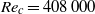The acoustic predictions are performed by the Ffowcs Williams & Hawkings (FWH) acoustic analogy formulation and incorporate convective effects. Surface and volume integrations of dipole and quadrupole source terms appearing in the FWH equation are performed using a three-dimensional wideband multi-level adaptive fast multipole method (FMM) in order to accelerate the calculations of aeroacoustic integrals. In order to validate the numerical solutions, flow simulation and acoustic prediction results are compared to experimental data available in the literature and good agreement is observed in terms of both aerodynamic and aeroacoustic results. For low-Mach-number flows, quadrupole sources can be neglected in the FWH equation and mean flow effects appear only for high frequencies. However, for higher speeds, convection effects are relevant for all frequencies and quadrupole sources have a more pronounced effect for medium and high frequencies. The convective effects are most readily observed in the upstream direction.

JFM classification

Acoustics: Aeroacoustics Turbulent Flows: Turbulent boundary layers Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 708 , 10 October 2012 , pp. 502 - 538
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Amiet, R. K. 1976 Noise due to turbulent flow past a trailing edge. J. Sound Vib. 47, 387–393.CrossRefGoogle Scholar
2. Beam, R. M. & Warming, R. F. 1978 An implicit factored scheme for the compressible Navier–Stokes equations. AIAA J. 16, 393–402.CrossRefGoogle Scholar
3. Bhaskaran, R. & Lele, S. K. 2010 Large eddy simulation of free stream turbulence effects on heat transfer to a high-pressure turbine cascade. J. Turbul. 11, 1–15.CrossRefGoogle Scholar
4. Blake, W. K. 1986 Mechanics of Flow-Induced Sound and Vibration, Volume II: Complex Flow-Structure Interactions. Academic Press.Google Scholar
5. Brooks, T. F. & Hodgson, T. H. 1981 Trailing edge noise prediction from measured surface pressures. J. Sound Vib. 78, 69–117.CrossRefGoogle Scholar
6. Brooks, T. F., Pope, D. S. & Marcolini, M. A. 1989 Airfoil self-noise and prediction. Tech. Rep. 1218 NASA Reference Publication.Google Scholar
7. Curle, N. 1955 The influence of solid boundaries upon aerodynamic sound. J. Fluid Mech. 231, 505–514.Google Scholar
8. Ewert, R., Appel, C., Dierke, J. & Herr, M. 2009. RANS/CAA based prediction of NACA0012 broadband trailing edge noise and experimental validation. AIAA Paper 2009-3269.CrossRefGoogle Scholar
9. Ffowcs-Williams, J. E. & Hall, L. H. 1970 Aerodynamic sound generation by turbulent flow in the vicinity of a scattering half plane. J. Fluid Mech. 40, 657–670.CrossRefGoogle Scholar
10. Ffowcs-Williams, J. E. & Hawkings, D. L. 1969 Sound generation by turbulence and surface in arbitrary motion. Phil. Trans. R. Soc. Lond. A 264, 321–342.Google Scholar
11. Gloerfelt, X. & Le Garrec, T. 2009. Trailing edge noise from an isolated aerofoil at a high Reynolds number. AIAA Paper 2009-3201.CrossRefGoogle Scholar
12. Gravante, S. P., Naguib, A. M., Wark, C. E. & Nagib, H. M. 1998 Characterization of the pressure fluctuations under a fully developed turbulent boundary layer. AIAA J. 36, 1808–1816.CrossRefGoogle Scholar
13. Herr, M 2007 Design criteria for low-noise trailing-edges. AIAA Paper 2007-3470.CrossRefGoogle Scholar
14. Herr, M, Appel, C., Dierke, J. & Ewert, R. 2010 Trailing-edge noise data quality assessment for CAA validation. AIAA Paper 2010-3877.CrossRefGoogle Scholar
15. Herr, M. & Dobrzynski, W. 2005 Experimental investigations in low-noise trailing-edge design. AIAA J. 43, 1167–1175.CrossRefGoogle Scholar
16. Howe, M. S. 1978 A review of the theory of trailing edge noise. J. Sound Vib. 61, 437–465.CrossRefGoogle Scholar
17. Howe, M. S. 2001 Edge-source acoustic Green’s function for an aerofoil of arbitrary chord with application to trailing-edge noise. Q. J. Mech. Appl. Maths. 54, 139–155.CrossRefGoogle Scholar
18. Hutcheson, F. V. & Brooks, T. F. 2004. Effects of angle of attack and velocity on trailing edge noise. AIAA Paper 2004-1031.CrossRefGoogle Scholar
19. Hwang, Y. F., Bonness, W. K. & Hambric, S. A. 2009 Comparison of semi-empirical models for turbulent boundary layer wall pressure spectra. J. Sound Vib. 319, 199–217.CrossRefGoogle Scholar
20. Jones, L. E. & Sandberg, R. D. 2011 Numerical analysis of tonal aerofoil self-noise and acoustic feedback-loops. J. Sound Vib. 330, 6137–6152.CrossRefGoogle Scholar
21. Jones, L. E., Sandham, N. D. & Sandberg, R. D. 2010 Acoustic source identification for transitional aerofoil flows using cross correlations. AIAA J. 48, 2299–2312.Google Scholar
22. Khalighi, Y., Mani, A., Ham, F. & Moin, P. 2010 Prediction of sound generated by complex flows at low Mach numbers. AIAA J. 48, 306–316.CrossRefGoogle Scholar
23. Le Garrec, T., Gloerfelt, X. & Corre, C. 2008 Direct noise computation of trailing edge noise at high Reynolds numbers. AIAA Paper 2008-2914.CrossRefGoogle Scholar
24. Lee, H. & Kang, S. H. 2000 Flow characteristics of transitional boundary layers on an aerofoil in wakes. Trans. ASME: J. Fluids Engng 122, 522–532.Google Scholar
25. Lele, S. J. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.CrossRefGoogle Scholar
26. Lilly, D. K. 1992 A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 4, 633–635.CrossRefGoogle Scholar
27. Lockard, D. P. 2000 An efficient, two-dimensional implementation of the Ffowcs Williams and Hawkings equation. J. Sound Vib. 229, 897–911.CrossRefGoogle Scholar
28. Lockard, D. P. & Lilley, G. M. 2004. The airframe noise reduction challenge. Tech. Rep. 213013. NASA Report.Google Scholar
29. Manoha, E., Troff, B. & Sagaut, P. 2000 Trailing-edge noise prediction using large-eddy simulation and acoustic analogy. AIAA J. 38, 575–583.CrossRefGoogle Scholar
30. Marsden, O., Bogey, C. & Bailly, C. 2008 Direct noise computation of the turbulent flow around a zero-incidence aerofoil. AIAA J. 46, 874–883.CrossRefGoogle Scholar
31. Moreau, S. & Roger, M. 2005 Effect of aerofoil aerodynamic loading on trailing-edge noise sources. AIAA J. 43, 41–52.CrossRefGoogle Scholar
32. Moreau, S. & Roger, M. 2009 Back-scattering correction and further extensions of Amiet’s trailing-edge noise model. Part II. Application. J. Sound Vib, 323, 397–425.CrossRefGoogle Scholar
33. Nagarajan, S., Lele, S. K. & Ferziger, J. H. 2003 A robust high-order method for large eddy simulation. J. Comput. Phys. 191, 392–419.CrossRefGoogle Scholar
34. Nagarajan, S., Lele, S. K. & Ferziger, J. H. 2007 Leading-edge effects in bypass transition. J. Fluid Mech. 572, 471–504.CrossRefGoogle Scholar
35. Oberai, A. A., Roknaldin, F. & Hughes, T. J. R. 2002 Computation of trailing-edge noise due to turbulent flow over an aerofoil. AIAA J. 40, 2206–2216.CrossRefGoogle Scholar
36. Roger, M. & Moreau, S. 2004 Broadband self-noise from loaded fan blades. AIAA J. 42, 536–544.CrossRefGoogle Scholar
37. Roger, M. & Moreau, S. 2005 Back-scattering correction and further extensions of Amiet’s trailing-edge noise model Part 1. Theory. J. Sound Vib. 286, 477–506.Google Scholar
38. Sagrado, A. G. & Hynes, T. 2012 Wall pressure sources near an aerofoil trailing edge under turbulent boundary layers. Fluids Struct. 30, 3–34.CrossRefGoogle Scholar
39. Sandberg, R. D. & Jones, L. E. 2011 Direct numerical simulations of low Reynolds number flow over aerofoils with trailing-edge serrations. J. Sound Vib. 330, 3818–3831.CrossRefGoogle Scholar
40. Sandberg, R. D., Jones, L. E. & Sandham, N. D. 2008 Direct numerical simulations of noise generated by turbulent flow over aerofoils. AIAA Paper 2008-2861.CrossRefGoogle Scholar
41. Singer, B. A., Brentner, K. S. & Lockard, D. P. 2000 Simulation of acoustic scattering from a trailing edge. J. Sound Vib. 230, 541–560.CrossRefGoogle Scholar
42. Spalart, P. R. & Watmuff, J. H. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradient. J. Fluid Mech. 249, 337–371.CrossRefGoogle Scholar
43. Wang, M. & Moin, P. 2000 Computation of trailing-edge flow and noise using large-eddy simulation. AIAA J. 38, 2201–2209.CrossRefGoogle Scholar
44. Winkler, J., Moreau, S. & Carolus, T. 2012 Airfoil trailing-edge blowing: Broadband noise prediction from large-eddy simulation. AIAA J. 50, 294–303.CrossRefGoogle Scholar
45. Wolf, W. R. 2011 Airfoil aeroacoustics: LES and acoustic analogy predictions. PhD thesis, Stanford University.Google Scholar
46. Wolf, W. R. & Lele, S. K. 2010 Acoustic analogy formulations accelerated by fast multipole method for two-dimensional aeroacoustic problems. AIAA J. 48, 2274–2285.CrossRefGoogle Scholar
47. Wolf, W. R. & Lele, S. K. 2011a Aeroacoustic integrals accelerated by fast multipole method. AIAA J. 49, 1466–1477.CrossRefGoogle Scholar
48. Wolf, W. R. & Lele, S. K. 2011b Wideband fast multipole boundary element method: Application to acoustic scattering from aerodynamic bodies. Intl J. Numer. Meth. Fluids 67, 2108–2129.CrossRefGoogle Scholar
49. Wolf, W. R. & Lele, S. K. 2012 Trailing edge noise predictions using compressible large eddy simulation and acoustic analogy. AIAA J. (in press).CrossRefGoogle Scholar
50. Yu, C., Wolf, W. R., Bhaskaran, R. & Lele, S. K. 2010a. Study of noise generated by a tandem cylinder configuration using LES and fast acoustic analogy formulations. Tech. Rep.. Workshop on Benchmark Problems for Airframe Noise Computations.Google Scholar
51. Yu, C., Wolf, W. R. & Lele, S. K. 2010b. Airframe noise predictions using large eddy simulation. Tech. Rep. High Performance Computing Conference.Google Scholar