Article contents
Control of circular cylinder flow using distributed passive jets
Published online by Cambridge University Press: 13 June 2018
Abstract
A wind tunnel study has been carried out to investigate flow control around a hollow circular cylinder using passive jets driven by naturally occurring pressure differences. Flow enters the cylinder through spanwise holes along the stagnation line and exits through a spanwise distribution of holes at 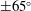 $\pm 65^{\circ }$ . The diameter of the entry and exit holes were 1 % and 0.5 % of the cylinder diameter, respectively. Reynolds numbers were at the upper end of the subcritical regime and ranged from
$\pm 65^{\circ }$ . The diameter of the entry and exit holes were 1 % and 0.5 % of the cylinder diameter, respectively. Reynolds numbers were at the upper end of the subcritical regime and ranged from 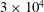 $3\times 10^{4}$ to
$3\times 10^{4}$ to 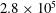 $2.8\times 10^{5}$ . Jet spacings of 10 % and 20 % of the cylinder diameter were investigated, and the ratio of the average jet exit velocity to the cross-flow velocity at the boundary layer edge was found to rise to approximately 0.35 and 0.4, respectively, above a Reynolds number of
$2.8\times 10^{5}$ . Jet spacings of 10 % and 20 % of the cylinder diameter were investigated, and the ratio of the average jet exit velocity to the cross-flow velocity at the boundary layer edge was found to rise to approximately 0.35 and 0.4, respectively, above a Reynolds number of 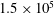 $1.5\times 10^{5}$ . Findings based on using the surface oil flow technique revealed a repeating, organised cellular pattern downstream of adjacent jet exit holes consisting of a primary counter-rotating vortex pair structure, followed by a secondary weaker pair. Downstream of adjacent exit holes, and centred midway between them, there exists a separation bubble which delays final flow separation compared with the flow directly downstream of a jet. The variation in the angular position of boundary layer separation across the span had the effect of suppressing von Kármán vortex shedding. This resulted in a drag coefficient, at the upper end of the Reynolds-number range studied, 14.5 % lower than that found using trip wires to initiate boundary layer transition.
$1.5\times 10^{5}$ . Findings based on using the surface oil flow technique revealed a repeating, organised cellular pattern downstream of adjacent jet exit holes consisting of a primary counter-rotating vortex pair structure, followed by a secondary weaker pair. Downstream of adjacent exit holes, and centred midway between them, there exists a separation bubble which delays final flow separation compared with the flow directly downstream of a jet. The variation in the angular position of boundary layer separation across the span had the effect of suppressing von Kármán vortex shedding. This resulted in a drag coefficient, at the upper end of the Reynolds-number range studied, 14.5 % lower than that found using trip wires to initiate boundary layer transition.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 13
- Cited by


