Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Min Yun, B.
Aidun, Cyrus K.
and
Yoganathan, Ajit P.
2014.
Blood Damage Through a Bileaflet Mechanical Heart Valve: A Quantitative Computational Study Using a Multiscale Suspension Flow Solver.
Journal of Biomechanical Engineering,
Vol. 136,
Issue. 10,
Yun, B. Min
McElhinney, Doff B.
Arjunon, Shiva
Mirabella, Lucia
Aidun, Cyrus K.
and
Yoganathan, Ajit P.
2014.
Computational simulations of flow dynamics and blood damage through a bileaflet mechanical heart valve scaled to pediatric size and flow.
Journal of Biomechanics,
Vol. 47,
Issue. 12,
p.
3169.
Yun, B. Min
Dasi, L. P.
Aidun, C. K.
and
Yoganathan, A. P.
2014.
Highly resolved pulsatile flows through prosthetic heart valves using the entropic lattice-Boltzmann method.
Journal of Fluid Mechanics,
Vol. 754,
Issue. ,
p.
122.
Querzoli, Giorgio
Fortini, Stefania
Espa, Stefania
Costantini, Martina
and
Sorgini, Francesca
2014.
Fluid dynamics of aortic root dilation in Marfan syndrome.
Journal of Biomechanics,
Vol. 47,
Issue. 12,
p.
3120.
Caiazzo, Alfonso
Guibert, Romain
Boudjemline, Younes
and
Vignon-Clementel, Irene E.
2015.
Blood Flow Simulations for the Design of Stented Valve Reducer in Enlarged Ventricular Outflow Tracts.
Cardiovascular Engineering and Technology,
Vol. 6,
Issue. 4,
p.
485.
Marom, Gil
2015.
Numerical Methods for Fluid–Structure Interaction Models of Aortic Valves.
Archives of Computational Methods in Engineering,
Vol. 22,
Issue. 4,
p.
595.
Sotiropoulos, Fotis
Le, Trung Bao
and
Gilmanov, Anvar
2016.
Fluid Mechanics of Heart Valves and Their Replacements.
Annual Review of Fluid Mechanics,
Vol. 48,
Issue. 1,
p.
259.
Haya, Laura
and
Tavoularis, Stavros
2016.
Effects of bileaflet mechanical heart valve orientation on fluid stresses and coronary flow.
Journal of Fluid Mechanics,
Vol. 806,
Issue. ,
p.
129.
Wang, Y.
Shu, C.
Yang, L.M.
and
Yuan, H.Z.
2016.
A decoupling multiple-relaxation-time lattice Boltzmann flux solver for non-Newtonian power-law fluid flows
.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 235,
Issue. ,
p.
20.
Stamou, A C
and
Buick, J M
2016.
An LBM based model for initial stenosis development in the carotid artery.
Journal of Physics A: Mathematical and Theoretical,
Vol. 49,
Issue. 19,
p.
195602.
Zakaria, Mohamad Shukri
Ismail, Farzad
Tamagawa, Masaaki
Aziz, Ahmad Fazli Abdul
Wiriadidjaja, Surjatin
Basri, Adi Azrif
and
Ahmad, Kamarul Arifin
2017.
Review of numerical methods for simulation of mechanical heart valves and the potential for blood clotting.
Medical & Biological Engineering & Computing,
Vol. 55,
Issue. 9,
p.
1519.
Haya, Laura
and
Tavoularis, Stavros
2017.
Comparison of in vitro flows past a mechanical heart valve in anatomical and axisymmetric aorta models.
Experiments in Fluids,
Vol. 58,
Issue. 6,
Gharaie, Saleh Hassanzadeh
Mosadegh, Bobak
and
Morsi, Yosry
2018.
In Vitro Validation of a Numerical Simulation of Leaflet Kinematics in a Polymeric Aortic Valve Under Physiological Conditions.
Cardiovascular Engineering and Technology,
Vol. 9,
Issue. 1,
p.
42.
Wei, Zhenglun Alan
Sonntag, Simon Johannes
Toma, Milan
Singh-Gryzbon, Shelly
and
Sun, Wei
2018.
Computational Fluid Dynamics Assessment Associated with Transcatheter Heart Valve Prostheses: A Position Paper of the ISO Working Group.
Cardiovascular Engineering and Technology,
Vol. 9,
Issue. 3,
p.
289.
Song, Yukun
Chen, Shuai
and
Liu, Fengming
2018.
The well-posedness of solution to a compressible non-Newtonian fluid with self-gravitational potential.
Open Mathematics,
Vol. 16,
Issue. 1,
p.
1466.
Yeh, Han Hung
Barannyk, Oleksandr
Grecov, Dana
and
Oshkai, Peter
2019.
The influence of hematocrit on the hemodynamics of artificial heart valve using fluid-structure interaction analysis.
Computers in Biology and Medicine,
Vol. 110,
Issue. ,
p.
79.
Liu, Zixiang
Zhu, Yuanzheng
Clausen, Jonathan R.
Lechman, Jeremy B.
Rao, Rekha R.
and
Aidun, Cyrus K.
2019.
Multiscale method based on coupled lattice‐Boltzmann and Langevin‐dynamics for direct simulation of nanoscale particle/polymer suspensions in complex flows.
International Journal for Numerical Methods in Fluids,
Vol. 91,
Issue. 5,
p.
228.
Bernaschi, Massimo
Melchionna, Simone
and
Succi, Sauro
2019.
Mesoscopic simulations at the physics-chemistry-biology interface.
Reviews of Modern Physics,
Vol. 91,
Issue. 2,
2020.
Artificial Intelligence for Computational Modeling of the Heart.
p.
211.
Mihalef, Viorel
Mansi, Tommaso
Rapaka, Saikiran
and
Passerini, Tiziano
2020.
Artificial Intelligence for Computational Modeling of the Heart.
p.
43.
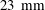 $23~ \mbox{mm}$ St. Jude Medical (SJM) Regent™ valve is selected for use in both the experiments and numerical simulations. The entropic lattice-Boltzmann method is used to simulate pulsatile flow through the valve with the inclusion of reverse leakage flow, while prescribing the flowrate and leaflet motion from experimental data. The numerical simulations are compared against experimental digital particle image velocimetry (DPIV) results from a previous study for validation. The numerical method is shown to match well with the experimental results quantitatively as well as qualitatively. Simulations are performed with efficient parallel processing at very high spatiotemporal resolution that can capture the finest details in the pulsatile BMHV flow field. This study validates the lattice-Boltzmann method as suitable for simulating pulsatile, high-Reynolds-number flows through prosthetic devices for use in future research.
$23~ \mbox{mm}$ St. Jude Medical (SJM) Regent™ valve is selected for use in both the experiments and numerical simulations. The entropic lattice-Boltzmann method is used to simulate pulsatile flow through the valve with the inclusion of reverse leakage flow, while prescribing the flowrate and leaflet motion from experimental data. The numerical simulations are compared against experimental digital particle image velocimetry (DPIV) results from a previous study for validation. The numerical method is shown to match well with the experimental results quantitatively as well as qualitatively. Simulations are performed with efficient parallel processing at very high spatiotemporal resolution that can capture the finest details in the pulsatile BMHV flow field. This study validates the lattice-Boltzmann method as suitable for simulating pulsatile, high-Reynolds-number flows through prosthetic devices for use in future research.
