Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tang, S. L.
Antonia, R. A.
Danaila, L.
Djenidi, L.
Zhou, T.
and
Zhou, Y.
2016.
Towards local isotropy of higher-order statistics in the intermediate wake.
Experiments in Fluids,
Vol. 57,
Issue. 7,
Ewing, D.
2017.
Two-point similarity in turbulent planar jet flows.
International Journal of Heat and Fluid Flow,
Vol. 67,
Issue. ,
p.
131.
Antonia, R. A.
Djenidi, L.
Danaila, L.
and
Tang, S. L.
2017.
Small scale turbulence and the finite Reynolds number effect.
Physics of Fluids,
Vol. 29,
Issue. 2,
Djenidi, Lyazid
Antonia, Robert A.
and
Danaila, Luminita
2017.
Self-preservation relation to the Kolmogorov similarity hypotheses.
Physical Review Fluids,
Vol. 2,
Issue. 5,
Djenidi, L.
Lefeuvre, N.
Kamruzzaman, M.
and
Antonia, R. A.
2017.
On the normalized dissipation parameter in decaying turbulence.
Journal of Fluid Mechanics,
Vol. 817,
Issue. ,
p.
61.
2018.
Retraction 17-00374.
Mechanical Engineering Reviews,
Vol. 5,
Issue. 1,
p.
17-00374.
Tang, S. L.
Djenidi, L.
Antonia, R. A.
and
Zhou, Y.
2018.
Secondary vortex street in the intermediate wake of a circular cylinder.
Experiments in Fluids,
Vol. 59,
Issue. 7,
Gauding, Michael
Wang, Lipo
Goebbert, Jens Henrik
Bode, Mathis
Danaila, Luminita
and
Varea, Emilien
2019.
On the self-similarity of line segments in decaying homogeneous isotropic turbulence.
Computers & Fluids,
Vol. 180,
Issue. ,
p.
206.
Djenidi, L.
Antonia, R. A.
and
Tang, S. L.
2019.
Scale invariance in finite Reynolds number homogeneous isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 864,
Issue. ,
p.
244.
Sarwar, Wasim
and
Mellibovsky, Fernando
2020.
Characterization of three-dimensional vortical structures in the wake past a circular cylinder in the transitional regime.
Physics of Fluids,
Vol. 32,
Issue. 7,
Kamruzzaman, Md.
Djenidi, Lyazid
and
Antonia, R. A.
2021.
Study of the interaction of two decaying grid-generated turbulent flows.
Physics of Fluids,
Vol. 33,
Issue. 9,
Gauding, M.
Bode, M.
Brahami, Y.
Varea, É.
and
Danaila, L.
2021.
Self-similarity of turbulent jet flows with internal and external intermittency.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Wei, Tie
Livescu, Daniel
and
Liu, Xiaofeng
2022.
Scaling patch analysis of planar turbulent wakes.
Physics of Fluids,
Vol. 34,
Issue. 6,
Jiang, Hongyi
Hu, Xiaoyuan
Cheng, Liang
and
Zhou, Tongming
2022.
Direct numerical simulation of the turbulent kinetic energy and energy dissipation rate in a cylinder wake.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Mandava, V.S.R.
Herrero, Joan
Kopp, Gregory A.
and
Giralt, Francesc
2022.
Wake behind a discontinuous cylinder: unveiling the role of the large scales in wake growth and entrainment.
Journal of Fluid Mechanics,
Vol. 936,
Issue. ,
Guimarães, Mateus C.
Pinho, Fernando T.
and
da Silva, Carlos B.
2022.
Turbulent planar wakes of viscoelastic fluids analysed by direct numerical simulations.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Álvarez, Antonio J.
Nieto, Félix
Kwok, Kenny K.C.S.
and
Hernández, Santiago
2023.
A simplified CFD approach for bluff-body aerodynamics under small scale free stream turbulent flow.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 241,
Issue. ,
p.
105500.
Cohen, Alexandre
Blais, Donovan
Mydlarski, Laurent
and
Baliga, B Rabi
2024.
Drag on circular cylinders with porous outer layers in turbulent cross-flow.
Fluid Dynamics Research,
Vol. 56,
Issue. 2,
p.
021401.
Jiang, Hongyi
2024.
On the absence of a secondary vortex street in three-dimensional and turbulent cylinder wakes.
Journal of Fluid Mechanics,
Vol. 993,
Issue. ,
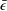 $\bar{{\it\epsilon}}$ on the wake axis. These SP solutions and the new
$\bar{{\it\epsilon}}$ on the wake axis. These SP solutions and the new 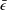 $\bar{{\it\epsilon}}$ relation are well supported by hot-wire data in the far wake at a Reynolds number of 2000 based on the free stream velocity and the cylinder diameter. On the far-wake axis, both the energy spectra and the structure functions exhibit an almost perfect collapse over all wavenumbers and separations, irrespective of the set of scaling variables used for normalisation. This is consistent with a complete self-preservation (i.e. SP is satisfied at all scales of motion) in the far wake.
$\bar{{\it\epsilon}}$ relation are well supported by hot-wire data in the far wake at a Reynolds number of 2000 based on the free stream velocity and the cylinder diameter. On the far-wake axis, both the energy spectra and the structure functions exhibit an almost perfect collapse over all wavenumbers and separations, irrespective of the set of scaling variables used for normalisation. This is consistent with a complete self-preservation (i.e. SP is satisfied at all scales of motion) in the far wake.

