Hostname: page-component-784d4fb959-9bxm5 Total loading time: 0 Render date: 2025-07-15T04:36:36.062Z Has data issue: false hasContentIssue false
  • English
  • Français

Combustion noise modelling of thermally perfect and multi-species gas flow in nozzles

Published online by Cambridge University Press:  11 July 2025

Yann Gentil Open the ORCID record for Yann Gentil [Opens in a new window] ,
Guillaume Daviller Open the ORCID record for Guillaume Daviller [Opens in a new window]  and
Stephane Moreau Open the ORCID record for Stephane Moreau [Opens in a new window]
Yann Gentil*
Affiliation:
CERFACS, 42 Avenue Gaspard Coriolis, Toulouse 31057, France
Guillaume Daviller
Affiliation:
CERFACS, 42 Avenue Gaspard Coriolis, Toulouse 31057, France
Stephane Moreau
Affiliation:
Department of Mechanical Engineering, University of Sherbrooke, Sherbrooke, QC J1K2R1, Canada
*
Corresponding author: Yann Gentil, gentil@cerfacs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

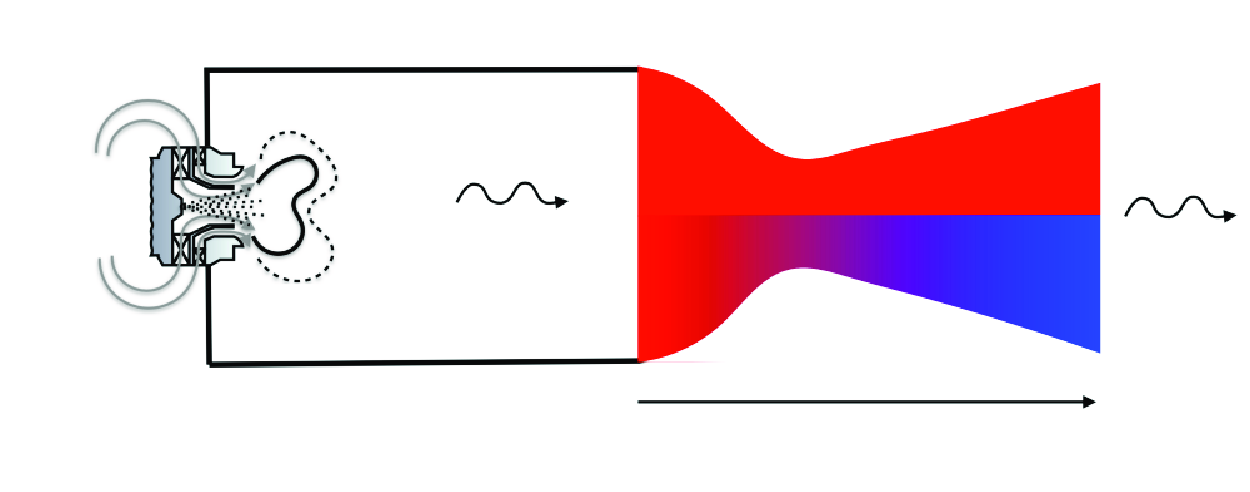
Several hypotheses are employed to describe the fluctuating motions within nozzles and to analytically predict combustion noise generation mechanisms. One of these assumptions is that of a calorifically perfect gas mixture, where $c_p$ is constant. Nonetheless, a realistic flow rather encompasses heat capacities $c_p$ that vary with temperature, i.e. $c_p = c_p(T)$, such that the mixture is called thermally perfect. The influence of the mixture assumptions on noise generation mechanisms is re-examined in this paper. To do so, the quasi one-dimensional Euler equations for multi-species, isentropic and non-reactive flow are considered within the nozzle. Their linearisation yields a new prediction model in addition to showing a new entropy-to-entropy coupling mechanism. Relying on either the assumption of low frequencies or the Magnus’ expansion methodology, two analytical solutions are derived and studied. Validation of these two prediction models is then provided relying on unsteady simulations of axisymmetric nozzles with superimposed incident waves. To generalise previous results, parametric studies are performed considering various nozzle flow geometries. Variations of up to $10\,\,\%$ are exhibited in a choked flow nozzle between the two mixtures, especially for the indirect entropy noise and the entropy-to-entropy transmission moduli.

JFM classification

Acoustics: Aeroacoustics Compressible Flows: Gas dynamics

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1014 , 10 July 2025 , A39
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bailly, C., Bogey, C. & Candel, S. 2010 Modelling of sound generation by turbulent reacting flows. Intl J. Aeroacoust. 9 (4–5), 461–489.CrossRefGoogle Scholar
Bauerheim, M., Duran, I., Livebardon, T., Wang, G., Moreau, S. & Poinsot, T. 2016 Transmission and reflection of acoustic and entropy waves through a stator–rotor stage. J. Sound Vib. 374, 260–278.CrossRefGoogle Scholar
Blanes, S., Casas, F., Oteo, J.A. & Ros, J. 2009 The Magnus expansion and some of its applications. Phys. Rep. 470 (5–6), 151–238.CrossRefGoogle Scholar
Colin, O. & Rudgyard, M. 2000 Development of high-order Taylor–Galerkin schemes for LES. J. Comput. Phys. 162 (2), 338–371.CrossRefGoogle Scholar
Cumpsty, N.A. & Marble, F.E. 1977 Interaction of entropy fluctuations with turbine blade rows; a mechanism of turbojet engine noise. Proc. R. Soc. Lond. Ser. A 357 (1690), 323–344.Google Scholar
De Domenico, F., Rolland, E.O. & Hochgreb, S. 2019 A generalised model for acoustic and entropic transfer function of nozzles with losses. J. Sound Vib. 440, 212–230.CrossRefGoogle Scholar
DeHoff, R.T. 1993 Thermodynamics in Material Science. McGraw-Hill.Google Scholar
Duran, I. & Moreau, S. 2013 Solution of the quasi-one-dimensional linearized Euler equations using flow invariants and the Magnus expansion. J. Fluid Mech. 723, 190–231.CrossRefGoogle Scholar
Duran, I. & Morgans, A.S. 2015 On the reflection and transmission of circumferential waves through nozzles. J. Fluid Mech. 773, 137–153.CrossRefGoogle Scholar
Duran Garcia-Rama, I. 2013 Prediction of combustion noise in modern aero engines combining LES and analytical methods. PhD thesis, Institut National Polytechnique de Toulouse (INP Toulouse).Google Scholar
European Environment Agency. 2020 Environmental Noise in Europe, 2020. Publications Office.Google Scholar
Gentil, Y., Daviller, G., Moreau, S. & Poinsot, T. 2024 a Multispecies flow indirect-noise modeling re-examined with a helicopter-engine application. AIAA J. 62 (4), 1536–1542.CrossRefGoogle Scholar
Gentil, Y., Daviller, G., Moreau, S., Treleaven, N.C.W. & Poinsot, T. 2024 b Theoretical analysis and numerical validation of the mechanisms controlling composition noise. J. Sound Vib. 585, 118463.CrossRefGoogle Scholar
Goh, C.S. & Morgans, A.S. 2011 Phase prediction of the response of choked nozzles to entropy and acoustic disturbances. J. Sound Vib. 330 (21), 5184–5198.CrossRefGoogle Scholar
Huet, M. 2017 Influence of calorically perfect gas assumption and thermal diffusion on indirect noise generation. In 24th International Congress On Sound and Vibration, ICSV 2017 (August).Google Scholar
Huet, M., Emmanuelli, A. & Ducruix, S. 2021 Influence of viscosity on entropy noise generation through a nozzle. J. Sound Vib. 510, 116293. (June).CrossRefGoogle Scholar
Huet, M. & Giauque, A. 2013 A nonlinear model for indirect combustion noise through a compact nozzle. J. Fluid Mech. 733 ( 2013), 268–301.CrossRefGoogle Scholar
Jain, A., Giusti, A. & Magri, L. 2023 Indirect noise from weakly reacting inhomogeneities. J. Fluid Mech. 965, 1–26.CrossRefGoogle Scholar
Jain, A. & Magri, L. 2022 A physical model for indirect noise in non-isentropic nozzles: transfer functions and stability. J. Fluid Mech. 935, 1–20. arXiv: 2106.10469.CrossRefGoogle Scholar
Leyko, M., Duran, I., Moreau, S., Nicoud, F. & Poinsot, T. 2014 Simulation and modelling of the waves transmission and generation in a stator blade row in a combustion-noise framework. J. Sound Vib. 333 (23), 6090–6106.CrossRefGoogle Scholar
Magri, L. 2017 On indirect noise in multicomponent nozzle flows. J. Fluid Mech. 828, 1–14.CrossRefGoogle Scholar
Magri, L., O’Brien, J. & Ihme, M. 2016 Compositional inhomogeneities as a source of indirect combustion noise. J. Fluid Mech. 799, R4.CrossRefGoogle Scholar
Marble, F.E. & Candel, S.M. 1977 Acoustic disturbance from gas non-uniformities convected through a nozzle. J. Sound Vib. 55 (2), 225–243.CrossRefGoogle Scholar
Morgans, A.S., Goh, C.S. & Dahan, J.A. 2013 The dissipation and shear dispersion of entropy waves in combustor thermoacoustics. J. Fluid Mech. 733, 1–10.CrossRefGoogle Scholar
Poinsot, T. & Veynante, D. 2012 Theorical and numerical combustion, 3rd edn.Google Scholar
Schønfeld, T. & Rudgyard, M. 1999 Steady and unsteady flow simulations using the hybrid flow solver AVBP. AIAA J. 37 (11), 1378–1385.CrossRefGoogle Scholar
Stow, S.R. & Dowling, A.P. 2001 Thermoacoustic oscillations in an annular combustor. In ASME Turbo Expo 2001: Power for Land, Sea, and Air. Available at: https://doi.org/10.1115/2001-GT-0037.CrossRefGoogle Scholar
Yeddula, S.R., Guzmán-Iñigo, J. & Morgans, A.S. 2022 a A solution for the quasi-one-dimensional linearised Euler equations with heat transfer. J. Fluid Mech. 936, 1–15. arXiv: 2201.10027.CrossRefGoogle Scholar
Yeddula, S.R., Guzmán-Iñigo, J. & Morgans, A.S. 2022 b Effect of steady and unsteady heat interactions on the acoustic and entropy transfer functions of a nozzle. In 28th AIAA/CEAS Aeroacoustics Conference, pp. 1–12. https://doi.org/10.2514/6.2022-2978.CrossRefGoogle Scholar
Yeddula, S.R., Guzmán-Iñigo, J., Morgans, A.S. & Yang, D. 2022 c A Magnus-expansion-based model for the sound generated by non-plane entropy perturbations passing through nozzles. In 28th AIAA/CEAS Aeroacoustics Conference, 2022. https://doi.org/10.2514/6.2022-2977.CrossRefGoogle Scholar