Article contents
Clustering of rapidly settling, low-inertia particle pairs in isotropic turbulence. Part 2. Comparison of theory and DNS
Published online by Cambridge University Press: 22 May 2019
Abstract
Part 1 (Rani et al. J. Fluid Mech., vol. 871, 2019, pp. 450–476) of this study presented a stochastic theory for the clustering of monodisperse, rapidly settling, low-Stokes-number particle pairs in homogeneous isotropic turbulence. The theory involved the development of closure approximations for the drift and diffusion fluxes in the probability density function (p.d.f.) equation for the pair relative positions  $\boldsymbol{r}$. In this part 2 paper, the theory is quantitatively analysed by comparing its predictions of particle clustering with data from direct numerical simulations (DNS) of isotropic turbulence containing particles settling under gravity. The simulations were performed at a Taylor micro-scale Reynolds number
$\boldsymbol{r}$. In this part 2 paper, the theory is quantitatively analysed by comparing its predictions of particle clustering with data from direct numerical simulations (DNS) of isotropic turbulence containing particles settling under gravity. The simulations were performed at a Taylor micro-scale Reynolds number 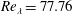 $Re_{\unicode[STIX]{x1D706}}=77.76$ for three Froude numbers
$Re_{\unicode[STIX]{x1D706}}=77.76$ for three Froude numbers 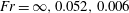 $Fr=\infty ,0.052,0.006$, where
$Fr=\infty ,0.052,0.006$, where 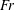 $Fr$ is the ratio of the Kolmogorov scale of acceleration and the magnitude of gravitational acceleration. Thus,
$Fr$ is the ratio of the Kolmogorov scale of acceleration and the magnitude of gravitational acceleration. Thus, 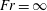 $Fr=\infty$ corresponds to zero gravity, and
$Fr=\infty$ corresponds to zero gravity, and 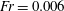 $Fr=0.006$ to the highest magnitude of gravity among the three DNS cases. For each
$Fr=0.006$ to the highest magnitude of gravity among the three DNS cases. For each 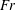 $Fr$, particles of Stokes numbers in the range
$Fr$, particles of Stokes numbers in the range 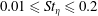 $0.01\leqslant St_{\unicode[STIX]{x1D702}}\leqslant 0.2$ were tracked in the DNS, and particle clustering quantified both as a function of separation and the spherical polar angle. We compared the DNS and theory values for the exponent
$0.01\leqslant St_{\unicode[STIX]{x1D702}}\leqslant 0.2$ were tracked in the DNS, and particle clustering quantified both as a function of separation and the spherical polar angle. We compared the DNS and theory values for the exponent 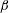 $\unicode[STIX]{x1D6FD}$ characterizing the power-law dependence of clustering on separation. The
$\unicode[STIX]{x1D6FD}$ characterizing the power-law dependence of clustering on separation. The 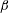 $\unicode[STIX]{x1D6FD}$ from the
$\unicode[STIX]{x1D6FD}$ from the 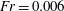 $Fr=0.006$ DNS case are in reasonable agreement with the theoretical predictions obtained using the second drift closure (referred to as DF2). To quantify the anisotropy in clustering, we calculated the leading–order coefficient in the spherical harmonics expansion of the p.d.f. of pair relative positions. The coefficients predicted by the theory (DF2) again show reasonable agreement with those calculated from the DNS clustering data for
$Fr=0.006$ DNS case are in reasonable agreement with the theoretical predictions obtained using the second drift closure (referred to as DF2). To quantify the anisotropy in clustering, we calculated the leading–order coefficient in the spherical harmonics expansion of the p.d.f. of pair relative positions. The coefficients predicted by the theory (DF2) again show reasonable agreement with those calculated from the DNS clustering data for 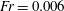 $Fr=0.006$. However, we note that in spite of the high magnitude of gravity, the clustering is only marginally anisotropic both in DNS and theory. The theory predicts that the spherical harmonic coefficient scales with
$Fr=0.006$. However, we note that in spite of the high magnitude of gravity, the clustering is only marginally anisotropic both in DNS and theory. The theory predicts that the spherical harmonic coefficient scales with 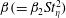 $\unicode[STIX]{x1D6FD}(=\unicode[STIX]{x1D6FD}_{2}St_{\unicode[STIX]{x1D702}}^{2})$, where
$\unicode[STIX]{x1D6FD}(=\unicode[STIX]{x1D6FD}_{2}St_{\unicode[STIX]{x1D702}}^{2})$, where 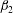 $\unicode[STIX]{x1D6FD}_{2}$ is the ratio of the drift and diffusion flux coefficients. Since the drift flux, and thereby
$\unicode[STIX]{x1D6FD}_{2}$ is the ratio of the drift and diffusion flux coefficients. Since the drift flux, and thereby 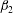 $\unicode[STIX]{x1D6FD}_{2}$, is seen to decrease with gravity for
$\unicode[STIX]{x1D6FD}_{2}$, is seen to decrease with gravity for 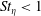 $St_{\unicode[STIX]{x1D702}}<1$, the anisotropy is also correspondingly diminished.
$St_{\unicode[STIX]{x1D702}}<1$, the anisotropy is also correspondingly diminished.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 7
- Cited by
Linked content
Please note that this article has a (1).

