Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Hao
Kolomenskiy, Dmitry
Nakata, Toshiyuki
and
Li, Gen
2017.
Unsteady bio-fluid dynamics in flying and swimming.
Acta Mechanica Sinica,
Vol. 33,
Issue. 4,
p.
663.
Chen, Di
Kolomenskiy, Dmitry
Nakata, Toshiyuki
and
Liu, Hao
2017.
Forewings match the formation of leading-edge vortices and dominate aerodynamic force production in revolving insect wings.
Bioinspiration & Biomimetics,
Vol. 13,
Issue. 1,
p.
016009.
Engels, Thomas
Kolomenskiy, Dmitry
Schneider, Kai
Farge, Marie
Lehmann, Fritz-Olaf
and
Sesterhenn, Jörn
2018.
Helical vortices generated by flapping wings of bumblebees.
Fluid Dynamics Research,
Vol. 50,
Issue. 1,
p.
011419.
Liu, Hao
Nakata, Toshiyuki
Noda, Ryusuke
Kolomenskiy, Dmitry
Chen, Di
Ueyama, Kouhei
Akiyama, Kazuki
and
Lakhtakia, Akhlesh
2018.
Robustness strategies in bio-inspired flight systems: morphology, dynamics, and flight control.
p.
27.
Jardin, T.
and
Colonius, T.
2018.
On the lift-optimal aspect ratio of a revolving wing at low Reynolds number.
Journal of The Royal Society Interface,
Vol. 15,
Issue. 143,
p.
20170933.
Chen, D.
Kolomenskiy, D.
Onishi, R.
and
Liu, H.
2018.
Versatile reduced-order model of leading-edge vortices on rotary wings.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Li, Chengyu
Dong, Haibo
and
Cheng, Bo
2020.
Tip vortices formation and evolution of rotating wings at low Reynolds numbers.
Physics of Fluids,
Vol. 32,
Issue. 2,
Terze, Zdravko
Pandža, Viktor
Andrić, Marijan
and
Zlatar, Dario
2022.
Reduced coupled flapping wing-fluid computational model with unsteady vortex wake.
Nonlinear Dynamics,
Vol. 109,
Issue. 2,
p.
975.
Zhang, Dong
Zhang, Jun-Duo
and
Huang, Wei-Xi
2022.
Physical models and vortex dynamics of swimming and flying: a review.
Acta Mechanica,
Vol. 233,
Issue. 4,
p.
1249.
Chen, Long
Cheng, Bo
and
Wu, Jianghao
2023.
Vorticity dynamics and stability of the leading-edge vortex on revolving wings.
Physics of Fluids,
Vol. 35,
Issue. 9,
Liu, Hao
Wang, Shizhao
and
Liu, Tianshu
2024.
Vortices and Forces in Biological Flight: Insects, Birds, and Bats.
Annual Review of Fluid Mechanics,
Vol. 56,
Issue. 1,
p.
147.
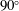 $90^{\circ }$ angle of attack, which is the simplest limiting case, yet shows remarkable similarity with the generally known leading-edge vortices. The problem is solved analytically, providing short closed-form expressions for the circulation and the position of the vortex. The good agreement with the numerical solution of the Navier–Stokes equations suggests that, for the conditions examined, the vorticity production at the sharp edge and its subsequent three-dimensional transport are the main effects that shape the edge vortex.
$90^{\circ }$ angle of attack, which is the simplest limiting case, yet shows remarkable similarity with the generally known leading-edge vortices. The problem is solved analytically, providing short closed-form expressions for the circulation and the position of the vortex. The good agreement with the numerical solution of the Navier–Stokes equations suggests that, for the conditions examined, the vorticity production at the sharp edge and its subsequent three-dimensional transport are the main effects that shape the edge vortex.

