Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sutherland, Peter
and
Melville, W. Kendall
2015.
Measuring Turbulent Kinetic Energy Dissipation at a Wavy Sea Surface.
Journal of Atmospheric and Oceanic Technology,
Vol. 32,
Issue. 8,
p.
1498.
Melville, W. Kendall
and
Fedorov, Alexey V.
2015.
The equilibrium dynamics and statistics of gravity–capillary waves.
Journal of Fluid Mechanics,
Vol. 767,
Issue. ,
p.
449.
Zonta, Francesco
Onorato, Miguel
and
Soldati, Alfredo
2016.
Decay of gravity-capillary waves in air/water sheared turbulence.
International Journal of Heat and Fluid Flow,
Vol. 61,
Issue. ,
p.
137.
Denner, Fabian
2016.
Frequency dispersion of small-amplitude capillary waves in viscous fluids.
Physical Review E,
Vol. 94,
Issue. 2,
Tang, Chenglong
Zhao, Jiaquan
Zhang, Peng
Law, Chung K.
and
Huang, Zuohua
2016.
Dynamics of internal jets in the merging of two droplets of unequal sizes.
Journal of Fluid Mechanics,
Vol. 795,
Issue. ,
p.
671.
Pizzo, N. E.
Deike, Luc
and
Melville, W. Kendall
2016.
Current generation by deep-water breaking waves.
Journal of Fluid Mechanics,
Vol. 803,
Issue. ,
p.
275.
Deike, Luc
Melville, W. Kendall
and
Popinet, Stéphane
2016.
Air entrainment and bubble statistics in breaking waves.
Journal of Fluid Mechanics,
Vol. 801,
Issue. ,
p.
91.
Deike, Luc
Pizzo, Nick
and
Melville, W. Kendall
2017.
Lagrangian transport by breaking surface waves.
Journal of Fluid Mechanics,
Vol. 829,
Issue. ,
p.
364.
Yang, Zixuan
Lu, Xin-Hua
Guo, Xin
Liu, Yi
and
Shen, Lian
2017.
Numerical simulation of sediment suspension and transport under plunging breaking waves.
Computers & Fluids,
Vol. 158,
Issue. ,
p.
57.
Denner, Fabian
Paré, Gounséti
and
Zaleski, Stéphane
2017.
Dispersion and viscous attenuation of capillary waves with finite amplitude.
The European Physical Journal Special Topics,
Vol. 226,
Issue. 6,
p.
1229.
Tang, Shuai
Yang, Zixuan
Liu, Caixi
Dong, Yu-Hong
and
Shen, Lian
2017.
Numerical Study on the Generation and Transport of Spume Droplets in Wind over Breaking Waves.
Atmosphere,
Vol. 8,
Issue. 12,
p.
248.
Deike, Luc
Lenain, Luc
and
Melville, W. Kendall
2017.
Air entrainment by breaking waves.
Geophysical Research Letters,
Vol. 44,
Issue. 8,
p.
3779.
Pizzo, Nick E.
2017.
Surfing surface gravity waves.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
p.
316.
Billingham, J.
Needham, D. J.
Korsukova, E.
and
Munro, R. J.
2018.
The initial development of a jet caused by fluid, body and free surface interaction. Part 5. Parasitic capillary waves on an initially horizontal surface.
Journal of Fluid Mechanics,
Vol. 836,
Issue. ,
p.
850.
Deike, Luc
Ghabache, Elisabeth
Liger-Belair, Gérard
Das, Arup K.
Zaleski, Stéphane
Popinet, Stéphane
and
Séon, Thomas
2018.
Dynamics of jets produced by bursting bubbles.
Physical Review Fluids,
Vol. 3,
Issue. 1,
Chen, Haifei
and
Zou, Qingping
2018.
Characteristics of Wave Breaking and Blocking by Spatially Varying Opposing Currents.
Journal of Geophysical Research: Oceans,
Vol. 123,
Issue. 5,
p.
3761.
Niewiarowski, Alexander
Adriaenssens, Sigrid
Pauletti, Ruy Marcelo
Addi, Khalid
and
Deike, Luc
2018.
Modeling underwater cable structures subject to breaking waves.
Ocean Engineering,
Vol. 164,
Issue. ,
p.
199.
De Vita, Francesco
Verzicco, Roberto
and
Iafrati, Alessandro
2018.
Breaking of modulated wave groups: kinematics and energy dissipation processes.
Journal of Fluid Mechanics,
Vol. 855,
Issue. ,
p.
267.
Hao, Xuanting
Cao, Tao
Yang, Zixuan
Li, Tianyi
and
Shen, Lian
2018.
Simulation-based study of wind-wave interaction.
Procedia IUTAM,
Vol. 26,
Issue. ,
p.
162.
Melville, W. Kendall
2018.
Wind-Wave Breaking.
Procedia IUTAM,
Vol. 26,
Issue. ,
p.
30.
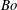 $\mathit{Bo}$ , and the initial wave steepness,
$\mathit{Bo}$ , and the initial wave steepness,  ${\it\epsilon}$ , is performed at a relatively high Reynolds number. The onset of wave breaking as a function of these two parameters is determined and a phase diagram in terms of
${\it\epsilon}$ , is performed at a relatively high Reynolds number. The onset of wave breaking as a function of these two parameters is determined and a phase diagram in terms of 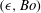 $({\it\epsilon},\mathit{Bo})$ is presented that distinguishes between non-breaking gravity waves, parasitic capillaries on a gravity wave, spilling breakers and plunging breakers. At high Bond number, a critical steepness
$({\it\epsilon},\mathit{Bo})$ is presented that distinguishes between non-breaking gravity waves, parasitic capillaries on a gravity wave, spilling breakers and plunging breakers. At high Bond number, a critical steepness 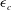 ${\it\epsilon}_{c}$ defines the onset of wave breaking. At low Bond number, the influence of surface tension is quantified through two boundaries separating, first gravity–capillary waves and breakers, and second spilling and plunging breakers; both boundaries scaling as
${\it\epsilon}_{c}$ defines the onset of wave breaking. At low Bond number, the influence of surface tension is quantified through two boundaries separating, first gravity–capillary waves and breakers, and second spilling and plunging breakers; both boundaries scaling as 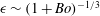 ${\it\epsilon}\sim (1+\mathit{Bo})^{-1/3}$ . Finally the wave energy dissipation is estimated for each wave regime and the influence of steepness and surface tension effects on the total wave dissipation is discussed. The breaking parameter
${\it\epsilon}\sim (1+\mathit{Bo})^{-1/3}$ . Finally the wave energy dissipation is estimated for each wave regime and the influence of steepness and surface tension effects on the total wave dissipation is discussed. The breaking parameter 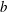 $b$ is estimated and is found to be in good agreement with experimental results for breaking waves. Moreover, the enhanced dissipation by parasitic capillaries is consistent with the dissipation due to breaking waves.
$b$ is estimated and is found to be in good agreement with experimental results for breaking waves. Moreover, the enhanced dissipation by parasitic capillaries is consistent with the dissipation due to breaking waves.
