Article contents
Bridging the gap between particle-scale forces and continuum modelling of size segregation: application to bedload transport
Published online by Cambridge University Press: 12 April 2021
Abstract
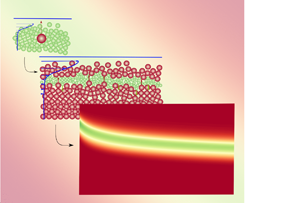
Gravity-driven size segregation is important in mountain streams where a wide range of grain sizes are transported as bedload. More particularly, vertical size segregation is a multi-scale process that originates in interactions at the scale of particles with important morphological consequences for the river bed. To address this issue, a volume-averaged multi-phase flow model for immersed bi-disperse granular flows was developed based on an interparticle segregation force (Guillard et al., J. Fluid Mech., vol. 807, 2016, R1) and a granular Stokesian drag force (Tripathi & Khakhar, J. Fluid Mech., vol. 717, 2013, pp. 643–669). An advection–diffusion model was derived from this model yielding parametrisations for the advection and diffusion coefficients based on the interparticle interactions. This approach makes it possible to bridge the gap between grain-scale physics and continuum modelling. Both models were successfully tested against existing discrete element model (DEM) simulations of size segregation in bedload transport (Chassagne et al., J. Fluid Mech., vol. 895, 2020, A30). Through a detailed investigation of the granular forces, it is demonstrated that the observed scaling of the advection and diffusion coefficients with the inertial number can be explained by the granular drag force dependency on the viscosity. The drag coefficient is shown to be linearly dependent on the small particle concentration. A new scaling relationship for the segregation force including the small particle concentration and the pressure is proposed. Lastly, adding a size-ratio dependency in the segregation force fairly reproduces the DEM results for a large range of small particle concentrations and size ratios.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 12
- Cited by


