Article contents
Boundary layer transition mechanismsbehind a micro-ramp
Published online by Cambridge University Press: 14 March 2016
Abstract
The early stage of three-dimensional laminar-to-turbulent transition behind a micro-ramp is studied in the incompressible regime using tomographic particle image velocimetry. Experiments are conducted at supercritical micro-ramp height 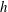 $h$ based Reynolds number
$h$ based Reynolds number 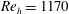 $Re_{h}=1170$ . The measurement domain encompasses 6 ramp widths spanwise and 73 ramp heights streamwise. The mean flow topology reveals the underlying vortex structure of the wake flow with multiple pairs of streamwise counter-rotating vortices visualized by streamwise vorticity. The primary pair generates a vigorous upwash motion in the symmetry plane with a pronounced momentum deficit. A secondary vortex pair is induced closer to the wall. The tertiary and even further vortices maintain a streamwise orientation, but are produced progressively outwards of the secondary pair and follow a wedge-type pattern. The instantaneous flow pattern reveals that the earliest unstable mode of the wake features arc-like Kelvin–Helmholtz (K–H) vortices in the separated shear layer. Under the influence of the K–H vortices, the wake exhibits a high level of fluctuations with a pulsatile mode for the streamwise momentum deficit. The K–H vortices are lifted up due to the upwash induced by the quasi-streamwise vortex pair, while they appear to undergo pairing, distortion and finally breakdown. Immediately downstream, a streamwise interval of relatively low vortical activity separates the end of the K–H region from the formation of new hairpin vortices close to the wall. The latter vortex structures originate from the region of maximum wall shear, induced by the secondary vortex pair causing strong ejection events which transport low-speed flow upwards. The whole pattern features a cascade of hairpin vortices along a turbulent/non-turbulent interface. The wedge-shaped cascade signifies the formation of a turbulent wedge. The turbulent properties of the wake are inspected with the spatial distribution of the velocity fluctuations and turbulence production in the developing boundary layer. Inside the wedge region, the velocity fluctuations approach quasi-spanwise homogeneity, indicating the development towards a turbulent boundary layer. The wedge interface is characterized by a localized higher level of velocity fluctuations and turbulence production, associated to the deflection of the shear layer close to the wall and the onset of coherent hairpin vortices inducing localized large-scale ejections.
$Re_{h}=1170$ . The measurement domain encompasses 6 ramp widths spanwise and 73 ramp heights streamwise. The mean flow topology reveals the underlying vortex structure of the wake flow with multiple pairs of streamwise counter-rotating vortices visualized by streamwise vorticity. The primary pair generates a vigorous upwash motion in the symmetry plane with a pronounced momentum deficit. A secondary vortex pair is induced closer to the wall. The tertiary and even further vortices maintain a streamwise orientation, but are produced progressively outwards of the secondary pair and follow a wedge-type pattern. The instantaneous flow pattern reveals that the earliest unstable mode of the wake features arc-like Kelvin–Helmholtz (K–H) vortices in the separated shear layer. Under the influence of the K–H vortices, the wake exhibits a high level of fluctuations with a pulsatile mode for the streamwise momentum deficit. The K–H vortices are lifted up due to the upwash induced by the quasi-streamwise vortex pair, while they appear to undergo pairing, distortion and finally breakdown. Immediately downstream, a streamwise interval of relatively low vortical activity separates the end of the K–H region from the formation of new hairpin vortices close to the wall. The latter vortex structures originate from the region of maximum wall shear, induced by the secondary vortex pair causing strong ejection events which transport low-speed flow upwards. The whole pattern features a cascade of hairpin vortices along a turbulent/non-turbulent interface. The wedge-shaped cascade signifies the formation of a turbulent wedge. The turbulent properties of the wake are inspected with the spatial distribution of the velocity fluctuations and turbulence production in the developing boundary layer. Inside the wedge region, the velocity fluctuations approach quasi-spanwise homogeneity, indicating the development towards a turbulent boundary layer. The wedge interface is characterized by a localized higher level of velocity fluctuations and turbulence production, associated to the deflection of the shear layer close to the wall and the onset of coherent hairpin vortices inducing localized large-scale ejections.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 49
- Cited by


