Article contents
Boundary integral formulation for flows containing an interface between two porous media
Published online by Cambridge University Press: 28 February 2017
Abstract
A system of boundary integral equations is derived for flows in domains composed of a porous medium of permeability 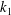 $k_{1}$ , surrounded by another porous medium of different permeability,
$k_{1}$ , surrounded by another porous medium of different permeability, 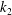 $k_{2}$ . The incompressible Brinkman equation is used to describe the flow in the porous media. We first apply a boundary integral representation of the Brinkman flow on each side of the dividing interface, and impose continuity of the velocity at the interface to derive the final formulation in terms of the interfacial velocity and surface forces. We discuss relations between the surface stresses based on the additional conditions imposed at the interface that depend on the porosity and permeability of the media and the structural composition of the interface. We present simulated results for test problems and different interface stress conditions. The results show significant sensitivity to the choice of the interface conditions, especially when the permeability is large. Since the Brinkman equation approaches the Stokes equation when the permeability approaches infinity, our boundary integral formulation can also be used to model the flow in sub-categories of Stokes–Stokes and Stokes–Brinkman configurations by considering infinite permeability in the Stokes fluid domain.
$k_{2}$ . The incompressible Brinkman equation is used to describe the flow in the porous media. We first apply a boundary integral representation of the Brinkman flow on each side of the dividing interface, and impose continuity of the velocity at the interface to derive the final formulation in terms of the interfacial velocity and surface forces. We discuss relations between the surface stresses based on the additional conditions imposed at the interface that depend on the porosity and permeability of the media and the structural composition of the interface. We present simulated results for test problems and different interface stress conditions. The results show significant sensitivity to the choice of the interface conditions, especially when the permeability is large. Since the Brinkman equation approaches the Stokes equation when the permeability approaches infinity, our boundary integral formulation can also be used to model the flow in sub-categories of Stokes–Stokes and Stokes–Brinkman configurations by considering infinite permeability in the Stokes fluid domain.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 11
- Cited by


