Article contents
Balanced solutions for an ellipsoidal vortex in a rotating stratified flow
Published online by Cambridge University Press: 03 August 2016
Abstract
We consider the motion of a single ellipsoidal vortex with uniform potential vorticity in a rotating stratified fluid at finite Rossby number  $\unicode[STIX]{x1D716}$ . Building on previous solutions obtained under the quasi-geostrophic approximation (at first order in
$\unicode[STIX]{x1D716}$ . Building on previous solutions obtained under the quasi-geostrophic approximation (at first order in  $\unicode[STIX]{x1D716}$ ), we obtain analytical solutions for the balanced part of the flow at
$\unicode[STIX]{x1D716}$ ), we obtain analytical solutions for the balanced part of the flow at  $O(\unicode[STIX]{x1D716}^{2})$ . These solutions capture important ageostrophic effects giving rise to an asymmetry in the evolution of cyclonic and anticyclonic vortices. Previous work has shown that, if the velocity field induced by an ellipsoidal vortex only depends linearly on spatial coordinates inside the vortex, i.e.
$O(\unicode[STIX]{x1D716}^{2})$ . These solutions capture important ageostrophic effects giving rise to an asymmetry in the evolution of cyclonic and anticyclonic vortices. Previous work has shown that, if the velocity field induced by an ellipsoidal vortex only depends linearly on spatial coordinates inside the vortex, i.e. 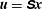 $\boldsymbol{u}=\unicode[STIX]{x1D64E}\boldsymbol{x}$ , then the dynamics reduces markedly to a simple matrix equation. The instantaneous vortex shape and orientation are encapsulated in a symmetric
$\boldsymbol{u}=\unicode[STIX]{x1D64E}\boldsymbol{x}$ , then the dynamics reduces markedly to a simple matrix equation. The instantaneous vortex shape and orientation are encapsulated in a symmetric 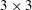 $3\times 3$ matrix
$3\times 3$ matrix  $\unicode[STIX]{x1D63D}$ , which is acted upon by the flow matrix
$\unicode[STIX]{x1D63D}$ , which is acted upon by the flow matrix 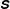 $\unicode[STIX]{x1D64E}$ to provide the vortex evolution. Under the quasi-geostrophic approximation, the flow matrix is determined by inverting the potential vorticity to obtain the streamfunction via Poisson’s equation, which has a known analytical solution depending on elliptic integrals. Here we show that higher-order balanced solutions, up to second order in the Rossby number, can also be calculated analytically. However, in this case there is a vector potential that requires the solution of three Poisson equations for each of its components. The source terms for these equations are independent of spatial coordinates within the ellipsoid, depending only on the elliptic integrals solved at the leading, quasi-geostrophic order. Unlike the quasi-geostrophic case, these source terms do not in general vanish outside the ellipsoid and have an inordinately complicated dependence on spatial coordinates. In the special case of an ellipsoid whose axes are aligned with the coordinate axes, we are able to derive these source terms and obtain the full analytical solution to the three Poisson equations. However, if one considers the homogeneous case, whereby the outer source terms are neglected, one can obtain an approximate solution having a compact matrix form analogous to the leading-order quasi-geostrophic case. This approximate solution proves to be highly accurate for the general case of an arbitrarily oriented ellipsoid, as verified through comparisons of the solutions with solutions obtained from numerical simulations of an ellipsoid using an accurate nonlinear balance model, even at moderate Rossby numbers.
$\unicode[STIX]{x1D64E}$ to provide the vortex evolution. Under the quasi-geostrophic approximation, the flow matrix is determined by inverting the potential vorticity to obtain the streamfunction via Poisson’s equation, which has a known analytical solution depending on elliptic integrals. Here we show that higher-order balanced solutions, up to second order in the Rossby number, can also be calculated analytically. However, in this case there is a vector potential that requires the solution of three Poisson equations for each of its components. The source terms for these equations are independent of spatial coordinates within the ellipsoid, depending only on the elliptic integrals solved at the leading, quasi-geostrophic order. Unlike the quasi-geostrophic case, these source terms do not in general vanish outside the ellipsoid and have an inordinately complicated dependence on spatial coordinates. In the special case of an ellipsoid whose axes are aligned with the coordinate axes, we are able to derive these source terms and obtain the full analytical solution to the three Poisson equations. However, if one considers the homogeneous case, whereby the outer source terms are neglected, one can obtain an approximate solution having a compact matrix form analogous to the leading-order quasi-geostrophic case. This approximate solution proves to be highly accurate for the general case of an arbitrarily oriented ellipsoid, as verified through comparisons of the solutions with solutions obtained from numerical simulations of an ellipsoid using an accurate nonlinear balance model, even at moderate Rossby numbers.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 13
- Cited by


