1. Introduction
Swimming confers on microorganisms the ability to find resources and favourable conditions in their environment (Guasto, Rusconi & Stocker Reference Guasto, Rusconi and Stocker2012). Marine microbes search for dissolved nutrients in the ocean (Stocker Reference Stocker2012) and porous sediments, and sperm seek out gametes in the reproductive tract (Fauci & Dillon Reference Fauci and Dillon2006). Owing to their random walk motility patterns, swimming bacteria readily disperse in quiescent fluids (Berg & Brown Reference Berg and Brown1972). This process is conveniently characterized by an effective diffusion coefficient that scales as  $D \sim v_s^2 \tau$. For example, Escherichia coli exhibits a swimming speed,
$D \sim v_s^2 \tau$. For example, Escherichia coli exhibits a swimming speed,  $v_s \approx 20$
$v_s \approx 20$  $\mathrm {\mu }$m s
$\mathrm {\mu }$m s $^{-1}$, and persistence (‘run’) time,
$^{-1}$, and persistence (‘run’) time,  $\tau \approx 1$ s, which gives rise to a diffusivity on a par with that of small molecules in water. A logical extension of this idea for imposed fluid flows – such as marine turbulence, groundwater and circulatory system flows – is to model the spreading of swimming microbes as an advection–diffusion process with effective diffusivity,
$\tau \approx 1$ s, which gives rise to a diffusivity on a par with that of small molecules in water. A logical extension of this idea for imposed fluid flows – such as marine turbulence, groundwater and circulatory system flows – is to model the spreading of swimming microbes as an advection–diffusion process with effective diffusivity,  $D$. However, this approach rapidly breaks down due to the coupling of microbial orientation to the flow, a phenomenon facilitated by cell shape and self-propulsion (Khurana & Ouellette Reference Khurana and Ouellette2012; Rusconi, Guasto & Stocker Reference Rusconi, Guasto and Stocker2014).
$D$. However, this approach rapidly breaks down due to the coupling of microbial orientation to the flow, a phenomenon facilitated by cell shape and self-propulsion (Khurana & Ouellette Reference Khurana and Ouellette2012; Rusconi, Guasto & Stocker Reference Rusconi, Guasto and Stocker2014).
The kinematics of microbial orientation,  $\boldsymbol {q}$, in flow are well described through Jeffery's equation (Pedley & Kessler Reference Pedley and Kessler1992) by parametrizing cells as prolate ellipsoids:
$\boldsymbol {q}$, in flow are well described through Jeffery's equation (Pedley & Kessler Reference Pedley and Kessler1992) by parametrizing cells as prolate ellipsoids:
where  $\boldsymbol {\omega }$ is the vorticity,
$\boldsymbol {\omega }$ is the vorticity,  $\boldsymbol{\mathsf{D}}$ is the rate-of-strain tensor and
$\boldsymbol{\mathsf{D}}$ is the rate-of-strain tensor and  $\varLambda$ is a constant that depends on the cell shape (
$\varLambda$ is a constant that depends on the cell shape ( $\varLambda = 0$ for spheres and
$\varLambda = 0$ for spheres and  $\varLambda \rightarrow 1$ for highly elongated objects). Random walk effects are commonly modelled by an additional rotational noise based on the cell's effective rotational diffusivity,
$\varLambda \rightarrow 1$ for highly elongated objects). Random walk effects are commonly modelled by an additional rotational noise based on the cell's effective rotational diffusivity,  $D_r \sim 1/\tau$. While a spherical swimmer rotates with the local vorticity, most bacteria are elongated (
$D_r \sim 1/\tau$. While a spherical swimmer rotates with the local vorticity, most bacteria are elongated ( $\varLambda \approx 1$), and thus their orientation,
$\varLambda \approx 1$), and thus their orientation,  $\boldsymbol {q}$, is drawn toward alignment with the extensional direction of the flow. In simple, steady, one-dimensional flows, the effects of cell alignment are readily observed in an Eulerian framework. For example in a Poiseuille flow, preferential bacterial orientation along the flow direction suppresses the effects of random motility across streamlines and causes accumulation in high-shear regions (Rusconi et al. Reference Rusconi, Guasto and Stocker2014).
$\boldsymbol {q}$, is drawn toward alignment with the extensional direction of the flow. In simple, steady, one-dimensional flows, the effects of cell alignment are readily observed in an Eulerian framework. For example in a Poiseuille flow, preferential bacterial orientation along the flow direction suppresses the effects of random motility across streamlines and causes accumulation in high-shear regions (Rusconi et al. Reference Rusconi, Guasto and Stocker2014).
In non-trivial, two-dimensional and time-dependent flows, microbes experience a complex time history of velocity gradients due to advection and swimming. A growing body of work has begun to identify the importance of a Lagrangian perspective in understanding these effects on microbial transport (Khurana & Ouellette Reference Khurana and Ouellette2012; Dehkharghani et al. Reference Dehkharghani, Waisbord, Dunkel and Guasto2019; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021; Si & Fang Reference Si and Fang2021). Specifically, hyperbolic Lagrangian coherent structures (LCSs) underlying these flows (Haller Reference Haller2015) are identified from the finite-time Lyapunov exponent (FTLE) field. These LCSs highlight regions of strong Lagrangian fluid stretching experienced by fluid particles during a fixed time history in the flow. The orientation and accumulation of elongated swimming bacteria strongly correlate with ridges of FTLE (manifolds), which are advective transport barriers to passive tracers (Dehkharghani et al. Reference Dehkharghani, Waisbord, Dunkel and Guasto2019; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021; Si & Fang Reference Si and Fang2021). Such hyperbolic LCSs have been crucial to our understanding of hindered and enhanced microbial transport in chaotic flows (Khurana & Ouellette Reference Khurana and Ouellette2012; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021) and anisotropic dispersion in porous media (Dehkharghani et al. Reference Dehkharghani, Waisbord, Dunkel and Guasto2019). However, these rich results are just beginning to scratch the surface of potential new insights into microbial transport afforded by LCS analysis. In particular, Ran & Arratia (Reference Ran and Arratia2024) investigate elliptical LCSs and examine the role of bacterial accumulation in reinforcing these transport barriers in chaotic flows.
2. Overview
In a two-dimensional, time-periodic flow, Ran & Arratia (Reference Ran and Arratia2024) experimentally measure the effects of a dilute suspension of swimming bacteria ( $\phi _b = 0.5\,\%$ volume fraction of E. coli) on the chaotic mixing of a passive scalar (dye). Stroboscopic imaging after each period,
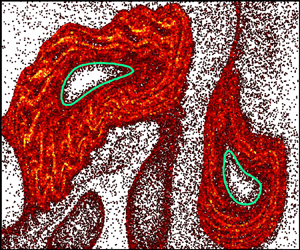
$\phi _b = 0.5\,\%$ volume fraction of E. coli) on the chaotic mixing of a passive scalar (dye). Stroboscopic imaging after each period,  $T$, of the flow reveals robust voids in the dye field, but only in the presence of bacteria (figure 1a,b). The dilute bulk bacterial concentration has only a minor impact on the measured velocity field. However, the presence of randomly swimming bacteria is expected to significantly increase the effective scalar diffusion (Kim & Breuer Reference Kim and Breuer2004), which is in stark contrast with the presence of voids indicative of decreased mixing. Furthermore, while voids in the dye field are reminiscent of vortex structures, they show little correspondence with the vorticity field (figure 1 of Ran & Arratia Reference Ran and Arratia2024).
$T$, of the flow reveals robust voids in the dye field, but only in the presence of bacteria (figure 1a,b). The dilute bulk bacterial concentration has only a minor impact on the measured velocity field. However, the presence of randomly swimming bacteria is expected to significantly increase the effective scalar diffusion (Kim & Breuer Reference Kim and Breuer2004), which is in stark contrast with the presence of voids indicative of decreased mixing. Furthermore, while voids in the dye field are reminiscent of vortex structures, they show little correspondence with the vorticity field (figure 1 of Ran & Arratia Reference Ran and Arratia2024).
Figure 1. (a,b) Dye concentration field with measured LVBs (green) exhibits enhanced barrier properties with swimming bacteria (b) compared with no bacteria (a). (c) Simulations suggest that hindered dye transport into Lagrangian vortices results from enhanced bacterial density ( $\rho _N/\rho _0$) outside LVBs. Adapted from Ran & Arratia (Reference Ran and Arratia2024).
$\rho _N/\rho _0$) outside LVBs. Adapted from Ran & Arratia (Reference Ran and Arratia2024).
To better understand the novel topological features of this system, Ran & Arratia (Reference Ran and Arratia2024) use the language of dynamical systems and examine the Poincaré map of the periodic flow field – i.e. periodically sampled particle trajectories in phase space. When sampled stroboscopically, fluid particle trajectories exhibit nested tori (figure 1 of Ran & Arratia Reference Ran and Arratia2024), which are a signature of elliptic LCSs (or Lagrangian coherent vortices). These LCSs are formally identified by measuring the trajectory rotation average:
which is the time-averaged angular velocity of a particle trajectory. Here,  $\dot {\boldsymbol {x}}_i$ is the velocity of a particle trajectory in the Poincaré map,
$\dot {\boldsymbol {x}}_i$ is the velocity of a particle trajectory in the Poincaré map,  $i$ is a given period,
$i$ is a given period,  $N$ is the total number of periods and
$N$ is the total number of periods and  $\langle \,{\cdot}\, \rangle$ is the inner product. The outermost convex contours of
$\langle \,{\cdot}\, \rangle$ is the inner product. The outermost convex contours of  $\overline {\textrm {TRA}}_0^N(\boldsymbol {x}_0)$ are termed Lagrangian vortex boundaries (LVBs). In contrast with extension-dominated hyperbolic LCSs, elliptic LCSs are characterized by strong rotation. The LVBs robustly identify regions devoid of dye (figure 1a,b) and correspond to convective transport barriers (Aksamit & Haller Reference Aksamit and Haller2022). The presence of bacteria clearly augments the LVB barrier strength, evidenced by reduced dye flux into the vortices (figure 2 of Ran & Arratia Reference Ran and Arratia2024), but their precise role in this process remains unclear.
$\overline {\textrm {TRA}}_0^N(\boldsymbol {x}_0)$ are termed Lagrangian vortex boundaries (LVBs). In contrast with extension-dominated hyperbolic LCSs, elliptic LCSs are characterized by strong rotation. The LVBs robustly identify regions devoid of dye (figure 1a,b) and correspond to convective transport barriers (Aksamit & Haller Reference Aksamit and Haller2022). The presence of bacteria clearly augments the LVB barrier strength, evidenced by reduced dye flux into the vortices (figure 2 of Ran & Arratia Reference Ran and Arratia2024), but their precise role in this process remains unclear.
Numerical simulations reveal that elongated swimmers accumulate outside Lagrangian vortices, suggesting a potential mechanism for hindered scalar transport in this system. The bacterial density cannot be directly imaged in these macroscale experiments, and instead, Ran & Arratia (Reference Ran and Arratia2024) simulate the motion of an ensemble of non-interacting cells. The bacterial kinematics are the sum of the measured flow field and self-propulsion,  $\dot {\boldsymbol {x}} = \boldsymbol {v}_f + v_s \boldsymbol {q}$, coupled with rotation (1.1). The striking results predict that elongated motile bacteria are repelled from the Lagrangian vortices and accumulate outside the LVBs (figure 1c), while non-motile bacteria accumulate in their centres (figure 3 of Ran & Arratia Reference Ran and Arratia2024). Similar to microbial interactions with hyperbolic LCSs, the authors demonstrate that bacterial accumulation is driven by preferential orientation tangent to LVBs (figure 4 of Ran & Arratia Reference Ran and Arratia2024). Coupled with swimming, cell alignment prevents migration into the vortex centres, suggesting that LVBs are also barriers to bacterial transport. Based on these simulations, the authors hypothesize that the enhancement of LVB barriers to scalar transport might be due to dye diffusion through the accumulated bacterial suspension, which acts as a porous medium (figure 5 of Ran & Arratia Reference Ran and Arratia2024). Curiously, the local bacterial density is elevated by an order of magnitude above the background (figure 1c). While such concentrated bacteria are expected to enhance mixing through collective cell motion (Peng, Liu & Cheng Reference Peng, Liu and Cheng2021), these effects might be suppressed by flow-induced alignment to LVBs.
$\dot {\boldsymbol {x}} = \boldsymbol {v}_f + v_s \boldsymbol {q}$, coupled with rotation (1.1). The striking results predict that elongated motile bacteria are repelled from the Lagrangian vortices and accumulate outside the LVBs (figure 1c), while non-motile bacteria accumulate in their centres (figure 3 of Ran & Arratia Reference Ran and Arratia2024). Similar to microbial interactions with hyperbolic LCSs, the authors demonstrate that bacterial accumulation is driven by preferential orientation tangent to LVBs (figure 4 of Ran & Arratia Reference Ran and Arratia2024). Coupled with swimming, cell alignment prevents migration into the vortex centres, suggesting that LVBs are also barriers to bacterial transport. Based on these simulations, the authors hypothesize that the enhancement of LVB barriers to scalar transport might be due to dye diffusion through the accumulated bacterial suspension, which acts as a porous medium (figure 5 of Ran & Arratia Reference Ran and Arratia2024). Curiously, the local bacterial density is elevated by an order of magnitude above the background (figure 1c). While such concentrated bacteria are expected to enhance mixing through collective cell motion (Peng, Liu & Cheng Reference Peng, Liu and Cheng2021), these effects might be suppressed by flow-induced alignment to LVBs.
3. Summary and perspective
The recent study by Ran & Arratia (Reference Ran and Arratia2024) complements previous works on hyperbolic LCSs by highlighting the importance of elliptic LCSs for microbial transport in rotation-dominated flows. They showed that the transport barrier properties of LVBs are enhanced by the addition of a small concentration of swimming bacteria, which inhibit scalar transport into Lagrangian vortex centres. This result is very surprising, because chaotic flows and randomly swimming bacteria are separately regarded to enhance mixing. Yet, together, mixing is locally suppressed, and the resulting transport proves to be far less than the sum of its parts. Importantly, the flow structures identified through this Lagrangian viewpoint are not obvious in the Eulerian frame, but they play a key role in regulating the transport of both microbes and passive scalars.
This thought-provoking study sparks new questions on both the fundamental mechanism of transport barrier enhancement by bacteria and the impact of these phenomena in natural systems. The experimental observation of transport barrier enhancement is quite convincing and consistent with simulations of bacterial accumulation around LVBs. However, the precise mechanism by which bacteria hinder scalar transport in Lagrangian vortices remains to be directly tested. Naturally occurring marine and physiological flows are inherently three-dimensional, and bacteria often exhibit a broad distribution of swimming speeds. Whether the observed microbial accumulation and transport barrier enhancement near LVBs have a similar efficacy in higher-dimensional systems or with polydisperse swimming motility is not yet known. The current work by Ran & Arratia (Reference Ran and Arratia2024) explores transport effects on a truly passive scalar, but most dissolved chemical species of interest to microbes – including nutrients and toxins – provoke a chemotactic response (Berg & Brown Reference Berg and Brown1972). Even in the absence of chemotaxis, the incomplete mixing of both bacteria and dissolved resources is expected to strongly modify uptake by osmotrophic cells (Taylor & Stocker Reference Taylor and Stocker2012). An important future aspect of this work will be to determine how bacterial accumulation and transport barrier phenomena manifest when bacterial motility is coupled to scalar field gradients through chemical attraction or repulsion (Stocker Reference Stocker2012). Such coupling could lead to more complex and dynamic topological features, further influencing microbial uptake and productivity.

 $\rho _N/\rho _0$) outside LVBs. Adapted from Ran & Arratia (2024).
$\rho _N/\rho _0$) outside LVBs. Adapted from Ran & Arratia (2024).


1. Introduction
Swimming confers on microorganisms the ability to find resources and favourable conditions in their environment (Guasto, Rusconi & Stocker Reference Guasto, Rusconi and Stocker2012). Marine microbes search for dissolved nutrients in the ocean (Stocker Reference Stocker2012) and porous sediments, and sperm seek out gametes in the reproductive tract (Fauci & Dillon Reference Fauci and Dillon2006). Owing to their random walk motility patterns, swimming bacteria readily disperse in quiescent fluids (Berg & Brown Reference Berg and Brown1972). This process is conveniently characterized by an effective diffusion coefficient that scales as $D \sim v_s^2 \tau$. For example, Escherichia coli exhibits a swimming speed,
$D \sim v_s^2 \tau$. For example, Escherichia coli exhibits a swimming speed,  $v_s \approx 20$
$v_s \approx 20$  $\mathrm {\mu }$m s
$\mathrm {\mu }$m s $^{-1}$, and persistence (‘run’) time,
$^{-1}$, and persistence (‘run’) time,  $\tau \approx 1$ s, which gives rise to a diffusivity on a par with that of small molecules in water. A logical extension of this idea for imposed fluid flows – such as marine turbulence, groundwater and circulatory system flows – is to model the spreading of swimming microbes as an advection–diffusion process with effective diffusivity,
$\tau \approx 1$ s, which gives rise to a diffusivity on a par with that of small molecules in water. A logical extension of this idea for imposed fluid flows – such as marine turbulence, groundwater and circulatory system flows – is to model the spreading of swimming microbes as an advection–diffusion process with effective diffusivity,  $D$. However, this approach rapidly breaks down due to the coupling of microbial orientation to the flow, a phenomenon facilitated by cell shape and self-propulsion (Khurana & Ouellette Reference Khurana and Ouellette2012; Rusconi, Guasto & Stocker Reference Rusconi, Guasto and Stocker2014).
$D$. However, this approach rapidly breaks down due to the coupling of microbial orientation to the flow, a phenomenon facilitated by cell shape and self-propulsion (Khurana & Ouellette Reference Khurana and Ouellette2012; Rusconi, Guasto & Stocker Reference Rusconi, Guasto and Stocker2014).
The kinematics of microbial orientation, $\boldsymbol {q}$, in flow are well described through Jeffery's equation (Pedley & Kessler Reference Pedley and Kessler1992) by parametrizing cells as prolate ellipsoids:
$\boldsymbol {q}$, in flow are well described through Jeffery's equation (Pedley & Kessler Reference Pedley and Kessler1992) by parametrizing cells as prolate ellipsoids:
where $\boldsymbol {\omega }$ is the vorticity,
$\boldsymbol {\omega }$ is the vorticity,  $\boldsymbol{\mathsf{D}}$ is the rate-of-strain tensor and
$\boldsymbol{\mathsf{D}}$ is the rate-of-strain tensor and  $\varLambda$ is a constant that depends on the cell shape (
$\varLambda$ is a constant that depends on the cell shape ( $\varLambda = 0$ for spheres and
$\varLambda = 0$ for spheres and  $\varLambda \rightarrow 1$ for highly elongated objects). Random walk effects are commonly modelled by an additional rotational noise based on the cell's effective rotational diffusivity,
$\varLambda \rightarrow 1$ for highly elongated objects). Random walk effects are commonly modelled by an additional rotational noise based on the cell's effective rotational diffusivity,  $D_r \sim 1/\tau$. While a spherical swimmer rotates with the local vorticity, most bacteria are elongated (
$D_r \sim 1/\tau$. While a spherical swimmer rotates with the local vorticity, most bacteria are elongated ( $\varLambda \approx 1$), and thus their orientation,
$\varLambda \approx 1$), and thus their orientation,  $\boldsymbol {q}$, is drawn toward alignment with the extensional direction of the flow. In simple, steady, one-dimensional flows, the effects of cell alignment are readily observed in an Eulerian framework. For example in a Poiseuille flow, preferential bacterial orientation along the flow direction suppresses the effects of random motility across streamlines and causes accumulation in high-shear regions (Rusconi et al. Reference Rusconi, Guasto and Stocker2014).
$\boldsymbol {q}$, is drawn toward alignment with the extensional direction of the flow. In simple, steady, one-dimensional flows, the effects of cell alignment are readily observed in an Eulerian framework. For example in a Poiseuille flow, preferential bacterial orientation along the flow direction suppresses the effects of random motility across streamlines and causes accumulation in high-shear regions (Rusconi et al. Reference Rusconi, Guasto and Stocker2014).
In non-trivial, two-dimensional and time-dependent flows, microbes experience a complex time history of velocity gradients due to advection and swimming. A growing body of work has begun to identify the importance of a Lagrangian perspective in understanding these effects on microbial transport (Khurana & Ouellette Reference Khurana and Ouellette2012; Dehkharghani et al. Reference Dehkharghani, Waisbord, Dunkel and Guasto2019; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021; Si & Fang Reference Si and Fang2021). Specifically, hyperbolic Lagrangian coherent structures (LCSs) underlying these flows (Haller Reference Haller2015) are identified from the finite-time Lyapunov exponent (FTLE) field. These LCSs highlight regions of strong Lagrangian fluid stretching experienced by fluid particles during a fixed time history in the flow. The orientation and accumulation of elongated swimming bacteria strongly correlate with ridges of FTLE (manifolds), which are advective transport barriers to passive tracers (Dehkharghani et al. Reference Dehkharghani, Waisbord, Dunkel and Guasto2019; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021; Si & Fang Reference Si and Fang2021). Such hyperbolic LCSs have been crucial to our understanding of hindered and enhanced microbial transport in chaotic flows (Khurana & Ouellette Reference Khurana and Ouellette2012; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021) and anisotropic dispersion in porous media (Dehkharghani et al. Reference Dehkharghani, Waisbord, Dunkel and Guasto2019). However, these rich results are just beginning to scratch the surface of potential new insights into microbial transport afforded by LCS analysis. In particular, Ran & Arratia (Reference Ran and Arratia2024) investigate elliptical LCSs and examine the role of bacterial accumulation in reinforcing these transport barriers in chaotic flows.
2. Overview
In a two-dimensional, time-periodic flow, Ran & Arratia (Reference Ran and Arratia2024) experimentally measure the effects of a dilute suspension of swimming bacteria ( $\phi _b = 0.5\,\%$ volume fraction of E. coli) on the chaotic mixing of a passive scalar (dye). Stroboscopic imaging after each period,
$\phi _b = 0.5\,\%$ volume fraction of E. coli) on the chaotic mixing of a passive scalar (dye). Stroboscopic imaging after each period,  $T$, of the flow reveals robust voids in the dye field, but only in the presence of bacteria (figure 1a,b). The dilute bulk bacterial concentration has only a minor impact on the measured velocity field. However, the presence of randomly swimming bacteria is expected to significantly increase the effective scalar diffusion (Kim & Breuer Reference Kim and Breuer2004), which is in stark contrast with the presence of voids indicative of decreased mixing. Furthermore, while voids in the dye field are reminiscent of vortex structures, they show little correspondence with the vorticity field (figure 1 of Ran & Arratia Reference Ran and Arratia2024).
$T$, of the flow reveals robust voids in the dye field, but only in the presence of bacteria (figure 1a,b). The dilute bulk bacterial concentration has only a minor impact on the measured velocity field. However, the presence of randomly swimming bacteria is expected to significantly increase the effective scalar diffusion (Kim & Breuer Reference Kim and Breuer2004), which is in stark contrast with the presence of voids indicative of decreased mixing. Furthermore, while voids in the dye field are reminiscent of vortex structures, they show little correspondence with the vorticity field (figure 1 of Ran & Arratia Reference Ran and Arratia2024).
Figure 1. (a,b) Dye concentration field with measured LVBs (green) exhibits enhanced barrier properties with swimming bacteria (b) compared with no bacteria (a). (c) Simulations suggest that hindered dye transport into Lagrangian vortices results from enhanced bacterial density ( $\rho _N/\rho _0$) outside LVBs. Adapted from Ran & Arratia (Reference Ran and Arratia2024).
$\rho _N/\rho _0$) outside LVBs. Adapted from Ran & Arratia (Reference Ran and Arratia2024).
To better understand the novel topological features of this system, Ran & Arratia (Reference Ran and Arratia2024) use the language of dynamical systems and examine the Poincaré map of the periodic flow field – i.e. periodically sampled particle trajectories in phase space. When sampled stroboscopically, fluid particle trajectories exhibit nested tori (figure 1 of Ran & Arratia Reference Ran and Arratia2024), which are a signature of elliptic LCSs (or Lagrangian coherent vortices). These LCSs are formally identified by measuring the trajectory rotation average:
which is the time-averaged angular velocity of a particle trajectory. Here, $\dot {\boldsymbol {x}}_i$ is the velocity of a particle trajectory in the Poincaré map,
$\dot {\boldsymbol {x}}_i$ is the velocity of a particle trajectory in the Poincaré map,  $i$ is a given period,
$i$ is a given period,  $N$ is the total number of periods and
$N$ is the total number of periods and  $\langle \,{\cdot}\, \rangle$ is the inner product. The outermost convex contours of
$\langle \,{\cdot}\, \rangle$ is the inner product. The outermost convex contours of  $\overline {\textrm {TRA}}_0^N(\boldsymbol {x}_0)$ are termed Lagrangian vortex boundaries (LVBs). In contrast with extension-dominated hyperbolic LCSs, elliptic LCSs are characterized by strong rotation. The LVBs robustly identify regions devoid of dye (figure 1a,b) and correspond to convective transport barriers (Aksamit & Haller Reference Aksamit and Haller2022). The presence of bacteria clearly augments the LVB barrier strength, evidenced by reduced dye flux into the vortices (figure 2 of Ran & Arratia Reference Ran and Arratia2024), but their precise role in this process remains unclear.
$\overline {\textrm {TRA}}_0^N(\boldsymbol {x}_0)$ are termed Lagrangian vortex boundaries (LVBs). In contrast with extension-dominated hyperbolic LCSs, elliptic LCSs are characterized by strong rotation. The LVBs robustly identify regions devoid of dye (figure 1a,b) and correspond to convective transport barriers (Aksamit & Haller Reference Aksamit and Haller2022). The presence of bacteria clearly augments the LVB barrier strength, evidenced by reduced dye flux into the vortices (figure 2 of Ran & Arratia Reference Ran and Arratia2024), but their precise role in this process remains unclear.
Numerical simulations reveal that elongated swimmers accumulate outside Lagrangian vortices, suggesting a potential mechanism for hindered scalar transport in this system. The bacterial density cannot be directly imaged in these macroscale experiments, and instead, Ran & Arratia (Reference Ran and Arratia2024) simulate the motion of an ensemble of non-interacting cells. The bacterial kinematics are the sum of the measured flow field and self-propulsion, $\dot {\boldsymbol {x}} = \boldsymbol {v}_f + v_s \boldsymbol {q}$, coupled with rotation (1.1). The striking results predict that elongated motile bacteria are repelled from the Lagrangian vortices and accumulate outside the LVBs (figure 1c), while non-motile bacteria accumulate in their centres (figure 3 of Ran & Arratia Reference Ran and Arratia2024). Similar to microbial interactions with hyperbolic LCSs, the authors demonstrate that bacterial accumulation is driven by preferential orientation tangent to LVBs (figure 4 of Ran & Arratia Reference Ran and Arratia2024). Coupled with swimming, cell alignment prevents migration into the vortex centres, suggesting that LVBs are also barriers to bacterial transport. Based on these simulations, the authors hypothesize that the enhancement of LVB barriers to scalar transport might be due to dye diffusion through the accumulated bacterial suspension, which acts as a porous medium (figure 5 of Ran & Arratia Reference Ran and Arratia2024). Curiously, the local bacterial density is elevated by an order of magnitude above the background (figure 1c). While such concentrated bacteria are expected to enhance mixing through collective cell motion (Peng, Liu & Cheng Reference Peng, Liu and Cheng2021), these effects might be suppressed by flow-induced alignment to LVBs.
$\dot {\boldsymbol {x}} = \boldsymbol {v}_f + v_s \boldsymbol {q}$, coupled with rotation (1.1). The striking results predict that elongated motile bacteria are repelled from the Lagrangian vortices and accumulate outside the LVBs (figure 1c), while non-motile bacteria accumulate in their centres (figure 3 of Ran & Arratia Reference Ran and Arratia2024). Similar to microbial interactions with hyperbolic LCSs, the authors demonstrate that bacterial accumulation is driven by preferential orientation tangent to LVBs (figure 4 of Ran & Arratia Reference Ran and Arratia2024). Coupled with swimming, cell alignment prevents migration into the vortex centres, suggesting that LVBs are also barriers to bacterial transport. Based on these simulations, the authors hypothesize that the enhancement of LVB barriers to scalar transport might be due to dye diffusion through the accumulated bacterial suspension, which acts as a porous medium (figure 5 of Ran & Arratia Reference Ran and Arratia2024). Curiously, the local bacterial density is elevated by an order of magnitude above the background (figure 1c). While such concentrated bacteria are expected to enhance mixing through collective cell motion (Peng, Liu & Cheng Reference Peng, Liu and Cheng2021), these effects might be suppressed by flow-induced alignment to LVBs.
3. Summary and perspective
The recent study by Ran & Arratia (Reference Ran and Arratia2024) complements previous works on hyperbolic LCSs by highlighting the importance of elliptic LCSs for microbial transport in rotation-dominated flows. They showed that the transport barrier properties of LVBs are enhanced by the addition of a small concentration of swimming bacteria, which inhibit scalar transport into Lagrangian vortex centres. This result is very surprising, because chaotic flows and randomly swimming bacteria are separately regarded to enhance mixing. Yet, together, mixing is locally suppressed, and the resulting transport proves to be far less than the sum of its parts. Importantly, the flow structures identified through this Lagrangian viewpoint are not obvious in the Eulerian frame, but they play a key role in regulating the transport of both microbes and passive scalars.
This thought-provoking study sparks new questions on both the fundamental mechanism of transport barrier enhancement by bacteria and the impact of these phenomena in natural systems. The experimental observation of transport barrier enhancement is quite convincing and consistent with simulations of bacterial accumulation around LVBs. However, the precise mechanism by which bacteria hinder scalar transport in Lagrangian vortices remains to be directly tested. Naturally occurring marine and physiological flows are inherently three-dimensional, and bacteria often exhibit a broad distribution of swimming speeds. Whether the observed microbial accumulation and transport barrier enhancement near LVBs have a similar efficacy in higher-dimensional systems or with polydisperse swimming motility is not yet known. The current work by Ran & Arratia (Reference Ran and Arratia2024) explores transport effects on a truly passive scalar, but most dissolved chemical species of interest to microbes – including nutrients and toxins – provoke a chemotactic response (Berg & Brown Reference Berg and Brown1972). Even in the absence of chemotaxis, the incomplete mixing of both bacteria and dissolved resources is expected to strongly modify uptake by osmotrophic cells (Taylor & Stocker Reference Taylor and Stocker2012). An important future aspect of this work will be to determine how bacterial accumulation and transport barrier phenomena manifest when bacterial motility is coupled to scalar field gradients through chemical attraction or repulsion (Stocker Reference Stocker2012). Such coupling could lead to more complex and dynamic topological features, further influencing microbial uptake and productivity.
Acknowledgements
J.S.G. is grateful to J.A. Neufeld, and P.E. Arratia and R. Ran (authors of Ran & Arratia Reference Ran and Arratia2024) for valuable feedback on a draft of this article.
Declaration of interests
The author reports no conflict of interest.