Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-27T02:45:11.233Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic theory of Mack-mode receptivity in hypersonic boundary layers due to interaction of a heating/cooling source and a freestream sound wave

Published online by Cambridge University Press:  22 May 2023

Lei Zhao Open the ORCID record for Lei Zhao [Opens in a new window] ,
Jianhong He  and
Ming Dong Open the ORCID record for Ming Dong [Opens in a new window]
Lei Zhao
Affiliation:
Department of Mechanics, Tianjin University, Tianjin 300072, PR China
Jianhong He
Affiliation:
Department of Mechanics, Tianjin University, Tianjin 300072, PR China
Ming Dong*
Affiliation:
State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China Sino-Russian Mathematics Center, Peking University, Beijing 100871, PR China
*
†Email address for correspondence: dongming@imech.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

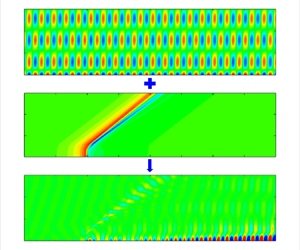
In this paper, we study the local receptivity of the inviscid Mack modes in hypersonic boundary layers induced by the interaction between a surface heating or cooling source (HCS) and a freestream acoustic wave. The asymptotic analysis reveals that among the three distinguished layers, i.e. the main, wall and Stokes layers, the leading-order receptivity is attributed to the interaction of the HCS-induced mean-flow distortion and the acoustic signature in the wall layer; the second-order contribution appears in the Stokes layer; the third-order contribution appears in both the main and wall layers. Interestingly, at a moderate Reynolds number, the third-order contribution to the receptivity efficiency may be quantitatively greater than the second-order one, but this does not lead to breakdown of this asymptotic theory. Assuming the HCS intensity to be sufficiently weak, the asymptotic predictions are made for four representative cases involving different Mach numbers and wall temperatures, which are compared with the results obtained by the finite-Reynolds-number theory based on either the extended compressible Orr–Sommerfeld equations or the harmonic linearised Navier–Stokes (HLNS) calculations. Taking into account the first three orders of the receptivity efficiency, the asymptotic predictions are confirmed to be sufficiently accurate even when the Reynolds number is a few thousands, and the agreement with the finite-Reynolds-number calculations is better when the wall temperature of the base flow approaches the adiabatic wall temperature. The HLNS calculations are also conducted for moderate HCS intensities. It is found that the nonlinearity does not affect the receptivity coefficient much even when the temperature distortion of the HCS reaches $80\,\%$ of the temperature at the wall.

JFM classification

Boundary Layers: Boundary layer receptivity Compressible Flows: Hypersonic Flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 963 , 25 May 2023 , A34
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bogolepov, V.V. 1977 Analysis of the limiting solutions for the case of supersonic viscous flow over small roughnesses on the body surface. Tr. TsAGI, No. 1812.Google Scholar
Cassel, K.W., Ruban, A.I. & Walker, J.D.A. 1996 The influence of wall cooling on hypersonic boundary-layer separation and stability. J. Fluid Mech. 321, 189–216.CrossRefGoogle Scholar
Chang, C. & Malik, M. 1994 Oblique-mode breakdown and secondary instability in supersonic boundary layers. J. Fluid Mech. 273, 323–360.CrossRefGoogle Scholar
Choudhari, M. & Duck, P.W. 1996 Nonlinear excitation of inviscid stationary vortex instabilities in a boundary-layer flow. In IUTAM Symposium on Nonlinear Instability and Transition in Three-Dimensional Boundary Layers. pp. 409–422.CrossRefGoogle Scholar
Choudhari, M. & Streett, C.L. 1992 A finite Reynolds-number approach for the prediction of boundary-layer receptivity in localized regions. Phys. Fluids A 4, 2495–2514.CrossRefGoogle Scholar
Crouch, J.D. 1992 Localized receptivity of boundary layers. Phys. Fluids A 4, 1408–1414.CrossRefGoogle Scholar
De Tullio, N. & Ruban, A.I. 2015 A numerical evaluation of the asymptotic theory of receptivity for subsonic compressible boundary layers. J. Fluid Mech. 771, 520–546.CrossRefGoogle Scholar
Dong, M. & Li, C. 2021 Effect of two-dimensional short rectangular indentations on hypersonic boundary-layer transition. AIAA J. 59, 2368–2381.CrossRefGoogle Scholar
Dong, M., Liu, Y. & Wu, X. 2020 Receptivity of inviscid modes in supersonic boundary layers due to scattering of freestream sound by wall roughness. J. Fluid Mech. 896, A23.CrossRefGoogle Scholar
Dong, M. & Zhang, A. 2018 Scattering of Tollmien–Schlichting waves as they pass over forward-/backward-facing steps. Appl. Maths Mech.-Engl. Ed. 39, 1411–1424.CrossRefGoogle Scholar
Dong, M. & Zhao, L. 2021 An asymptotic theory of the roughness impact on inviscid Mack modes in supersonic/hypersonic boundary layers. J. Fluid Mech. 913, A22.CrossRefGoogle Scholar
Duck, P.W., Ruban, A.I. & Zhikarev, C.N. 1996 Generation of Tollmien–Schlichting waves by free-stream turbulence. J. Fluid Mech. 312, 341–371.CrossRefGoogle Scholar
Fedorov, A.V. 2003 a Receptivity of a high-speed boundary layer to acoustic disturbances. J. Fluid Mech. 491, 101–129.CrossRefGoogle Scholar
Fedorov, A.V. 2003 b Receptivity of hypersonic boundary layer to acoustic disturbances scattered by surface roughness. AIAA Paper 2003-3731.CrossRefGoogle Scholar
Fedorov, A.V. 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–95.CrossRefGoogle Scholar
Fedorov, A.V. & Khokhlov, A.P. 1991 Excitation of unstable modes in a supersonic boundary layer by acoustic waves. Fluid Dyn. 9, 456–467.Google Scholar
Fedorov, A.V. & Khokhlov, A.P. 2001 Prehistory of instability in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 14, 359–375.CrossRefGoogle Scholar
Gao, J. & Luo, J.-S. 2014 Mode decomposition of nonlinear eigenvalue problems and application in flow stability. Appl. Maths Mech.-Engl. 35 (6), 667–674.CrossRefGoogle Scholar
Goldstein, M.E. 1983 The evolution of Tollmien–Schlichting waves near a leading edge. J. Fluid Mech. 127, 59–81.CrossRefGoogle Scholar
Goldstein, M.E. 1985 Scattering of acoustic waves into Tollmien–Schlichting waves by small streamwise variations in surface geometry. J. Fluid Mech. 154, 509–530.CrossRefGoogle Scholar
Goldstein, M.E. & Ricco, P. 2018 Non-localized boundary layer instabilities resulting from leading edge receptivity at moderate supersonic Mach numbers. J. Fluid Mech. 838, 435–477.CrossRefGoogle Scholar
Hader, C. & Fasel, H.F. 2019 Direct numerical simulations of hypersonic boundary-layer transition for a flared cone: fundamental breakdown. J Fluid Mech. 869, 341–384.CrossRefGoogle Scholar
Hatman, A.B., Hader, C. & Fasel, H.F. 2021 Nonlinear transition mechanism on a blunt cone at Mach 6: oblique breakdown. J Fluid Mech. 915, R2.CrossRefGoogle Scholar
Herbert, T. 1997 Parabolized stability equations. Annu. Rev. Fluid Mech. 29, 245–283.CrossRefGoogle Scholar
Jiang, X.Y., Lee, C.B., Chen, X., Smith, C.R. & Linden, P.F. 2020 Structure evolution at early stage of boundary-layer transition: simulation and experiment. J Fluid Mech. 890, A11.CrossRefGoogle Scholar
Kachanov, Y.S. 1994 Physical mechanisms of laminar–boundary-layer transition. Annu. Rev. Fluid Mech. 26, 411–482.CrossRefGoogle Scholar
Kara, K., Balakumar, P. & Kandil, O. 2011 Effects of nose bluntness on hypersonic boundary-layer receptivity and stability over cones. AIAA J. 49, 2593–2606.CrossRefGoogle Scholar
Lei, J. & Zhong, X. 2012 Linear stability analysis of nose bluntness effects on hypersonic boundary layer transition. J. Spacecr. Rockets 49, 24–37.CrossRefGoogle Scholar
Liu, Y., Dong, M. & Wu, X. 2020 Generation of first Mack modes in supersonic boundary layers by slow acoustic waves interacting with streamwise isolated wall roughness. J. Fluid Mech. 888, A10.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2003 Receptivity of a supersonic boundary layer over a flat plate. Part 1. Receptivity to free-stream sound. J. Fluid Mech. 488, 31–78.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2005 Receptivity of a supersonic boundary layer over a flat plate. Part 3. Effects of different types of free-stream disturbances. J. Fluid Mech. 532, 63–109.CrossRefGoogle Scholar
Mack, L. 1987 Review of linear compressible stability theory. In Stability of Time Dependent and Spatially Varying Flows (ed. D.L. Dwoyer & M.Y. Hussaini), pp. 164–187. Springer.CrossRefGoogle Scholar
Maslov, A.A., Shiplyuk, A.N., Sidorenko, A.A. & Arnal, D. 2001 Leading-edge receptivity of a hypersonic boundary layer on a flat plate. J. Fluid Mech. 426, 73–94.CrossRefGoogle Scholar
Morkovin, M.V. 1969 Critical evaluation of transition from laminar to turbulent shear layers with emphasis on hypersonically traveling bodies. Tech. Rep. AFFDL-TR, 68-149. US Air Force Flight Dynamics Laboratory, Wright-Patterson Air Force Base.Google Scholar
Neiland, V.Y., Bogolepov, V.V., Dudin, G.N. & Lipatov, I.I. 2008 Boundary layer flow over roughnesses at body surfaces. In Aerospace Engineering, Asymptotic Theory of Supersonic Viscous Gas Flows (ed. V.Ya. Neiland, V.V. Bogolepov, G.N. Dudin & I.I. Lipatov), pp. 433–508. Butterworth-Heinemann.CrossRefGoogle Scholar
Raposo, H., Mughal, S. & Ashworth, R. 2019 An adjoint compressible linearised Navier–Stokes approach to model generation of Tollmien–Schlichting waves by sound. J. Fluid Mech. 877, 105–129.CrossRefGoogle Scholar
Raposo, H., Mughal, S., Bensalah, A. & Ashworth, R. 2021 Acoustic–roughness receptivity in subsonic boundary-layer flows over aerofoils. J. Fluid Mech. 925, A7.CrossRefGoogle Scholar
Ruban, A.I. 1984 On Tollmien–Schlichting wave generation by sound (in Russian). Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 5, 44–52 (translation in Fluid Dyn. 19, 709–716).Google Scholar
Ruban, A.I., Kershari, S.K. & Kravtsova, M.A. 2021 On boundary-layer receptivity to entropy waves. J. Fluid Mech. 929, A17.CrossRefGoogle Scholar
Smith, F.T. 1989 On the first-mode instability in subsonic, supersonic or hypersonic boundary layers. J. Fluid Mech. 198, 127–153.CrossRefGoogle Scholar
Terent'ev, E.D. 1981 Linear problem for a vibrator in subsonic boundary layer (in Russian). Prikl. Mat. Mekh. 45, 1049–1055 (translation in J. Appl. Math. Mech. 45, 791–795. doi:10.1016/0021-8928(81)90120-9).Google Scholar
Terent'ev, E.D. 1984 The linear problem of a vibrator performing harmonic oscillations at supercritical frequencies in a subsonic boundary layer (in Russian). Prikl. Mat. Mekh. 48, 184–191 (translation in J. Appl. Math. Mech. 48, 184–191. doi:10.1016/0021-8928(84)90087-X).Google Scholar
Tumin, A. 2003 Multimode decomposition of spatially growing perturbations in a two-dimensional boundary layer. Phys. Fluids 15 (9), 2525–2540.CrossRefGoogle Scholar
Wan, B., Su, C. & Chen, J. 2020 Receptivity of a hypersonic blunt cone: role of disturbances in entropy layer. AIAA J. 58, 4047–4054.CrossRefGoogle Scholar
Wu, X. 2001 On local boundary-layer receptivity to vortical disturbances in the free-stream. J. Fluid Mech. 449, 373–393.CrossRefGoogle Scholar
Wu, X. & Dong, M. 2016 a Entrainment of short-wavelength free-stream vortical disturbances in compressible and incompressible boundary layers. J. Fluid Mech. 797, 683–782.CrossRefGoogle Scholar
Wu, X. & Dong, M. 2016 b A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition: transmission coefficient as an eigenvalue. J. Fluid Mech. 794, 68–108.CrossRefGoogle Scholar
Zhao, L. & Dong, M. 2020 Effect of suction on laminar-flow control in subsonic boundary layers with forward-/backward-facing steps. Phys. Fluids 32, 054108.Google Scholar
Zhao, L. & Dong, M. 2022 Effect of surface temperature strips on the evolution of supersonic and hypersonic Mack modes: asymptotic theory and numerical results. Phys. Rev. Fluids 7, 053901.CrossRefGoogle Scholar
Zhao, L., Dong, M. & Yang, Y. 2019 Harmonic linearized Navier–Stokes equation on describing the effect of surface roughness on hypersonic boundary-layer transition. Phys. Fluids 31, 034108.Google Scholar
Zhigulev, V.N. & Tumin, A.M. 1987 Onset of Turbulence: Dynamic Theory of the Excitation and Evolution of Instabilities in Boundary Layers (in Russian). Nauka.Google Scholar
Zhong, X. & Wang, X. 2012 Direct numerical simulation on the receptivity, instability and transition of hypersonic boundary layers. Annu. Rev. Fluid Mech. 44, 527–561.CrossRefGoogle Scholar