Article contents
Assessment of turbulence models using DNS data of compressible plane free shear layer flow
Published online by Cambridge University Press: 23 November 2021
Abstract
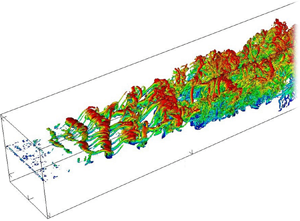
The present paper uses the detailed flow data produced by direct numerical simulation (DNS) of a three-dimensional, spatially developing plane free shear layer to assess several commonly used turbulence models in compressible flows. The free shear layer is generated by two parallel streams separated by a splitter plate, with a naturally developing inflow condition. The DNS is conducted using a high-order discontinuous spectral element method (DSEM) for various convective Mach numbers. The DNS results are employed to provide insights into turbulence modelling. The analyses show that with the knowledge of the Reynolds velocity fluctuations and averages, the considered strong Reynolds analogy models can accurately predict temperature fluctuations and Favre velocity averages, while the extended strong Reynolds analogy models can correctly estimate the Favre velocity fluctuations and the Favre shear stress. The pressure–dilatation correlation and dilatational dissipation models overestimate the corresponding DNS results, especially with high compressibility. The pressure–strain correlation models perform excellently for most pressure–strain correlation components, while the compressibility modification model gives poor predictions. The results of an a priori test for subgrid-scale (SGS) models are also reported. The scale similarity and gradient models, which are non-eddy viscosity models, can accurately reproduce SGS stresses in terms of structure and magnitude. The dynamic Smagorinsky model, an eddy viscosity model but based on the scale similarity concept, shows acceptable correlation coefficients between the DNS and modelled SGS stresses. Finally, the Smagorinsky model, a purely dissipative model, yields low correlation coefficients and unacceptable accumulated errors.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by


