Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hsieh, Chi-Wen
Chi, Po-Wei
Chen, Chih-Yen
Weng, Chun-Jen
and
Wang, Lijuan
2019.
Automatic Precipitation Measurement Based on Raindrop Imaging and Artificial Intelligence.
IEEE Transactions on Geoscience and Remote Sensing,
Vol. 57,
Issue. 12,
p.
10276.
Rabault, Jean
and
Kuhnle, Alexander
2019.
Accelerating deep reinforcement learning strategies of flow control through a multi-environment approach.
Physics of Fluids,
Vol. 31,
Issue. 9,
Nair, Aditya G.
Yeh, Chi-An
Kaiser, Eurika
Noack, Bernd R.
Brunton, Steven L.
and
Taira, Kunihiko
2019.
Cluster-based feedback control of turbulent post-stall separated flows.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
345.
Bucci, M. A.
Semeraro, O.
Allauzen, A.
Wisniewski, G.
Cordier, L.
and
Mathelin, L.
2019.
Control of chaotic systems by deep reinforcement learning.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 475,
Issue. 2231,
p.
20190351.
Belus, Vincent
Rabault, Jean
Viquerat, Jonathan
Che, Zhizhao
Hachem, Elie
and
Reglade, Ulysse
2019.
Exploiting locality and translational invariance to design effective deep reinforcement learning control of the 1-dimensional unstable falling liquid film.
AIP Advances,
Vol. 9,
Issue. 12,
Beintema, Gerben
Corbetta, Alessandro
Biferale, Luca
and
Toschi, Federico
2020.
Controlling Rayleigh–Bénard convection via reinforcement learning.
Journal of Turbulence,
Vol. 21,
Issue. 9-10,
p.
585.
Milan, Petro Junior
Wang, Xingjian
Hickey, Jean-Pierre
Li, Yixing
and
Yang, Vigor
2020.
Accelerating Numerical Simulations of Supercritical Fluid Flows using Deep Neural Networks.
Brunton, Steven L.
Noack, Bernd R.
and
Koumoutsakos, Petros
2020.
Machine Learning for Fluid Mechanics.
Annual Review of Fluid Mechanics,
Vol. 52,
Issue. 1,
p.
477.
Eivazi, Hamidreza
Veisi, Hadi
Naderi, Mohammad Hossein
and
Esfahanian, Vahid
2020.
Deep neural networks for nonlinear model order reduction of unsteady flows.
Physics of Fluids,
Vol. 32,
Issue. 10,
Xu, Hui
Zhang, Wei
Deng, Jian
and
Rabault, Jean
2020.
Active flow control with rotating cylinders by an artificial neural network trained by deep reinforcement learning.
Journal of Hydrodynamics,
Vol. 32,
Issue. 2,
p.
254.
Du, Xiangxi
Sun, Yanhua
and
Lv, Zhihan
2020.
Control of hybrid electromagnetic bearing and elastic foil gas bearing under deep learning.
PLOS ONE,
Vol. 15,
Issue. 12,
p.
e0243107.
Frank, Michael
Drikakis, Dimitris
and
Charissis, Vassilis
2020.
Machine-Learning Methods for Computational Science and Engineering.
Computation,
Vol. 8,
Issue. 1,
p.
15.
Pawar, Suraj
Ahmed, Shady E.
San, Omer
and
Rasheed, Adil
2020.
Data-driven recovery of hidden physics in reduced order modeling of fluid flows.
Physics of Fluids,
Vol. 32,
Issue. 3,
Tokarev, Mikhail
Palkin, Egor
and
Mullyadzhanov, Rustam
2020.
Deep Reinforcement Learning Control of Cylinder Flow Using Rotary Oscillations at Low Reynolds Number.
Energies,
Vol. 13,
Issue. 22,
p.
5920.
Rabault, Jean
Ren, Feng
Zhang, Wei
Tang, Hui
and
Xu, Hui
2020.
Deep reinforcement learning in fluid mechanics: A promising method for both active flow control and shape optimization.
Journal of Hydrodynamics,
Vol. 32,
Issue. 2,
p.
234.
Han, Bing-Zheng
and
Huang, Wei-Xi
2020.
Active control for drag reduction of turbulent channel flow based on convolutional neural networks.
Physics of Fluids,
Vol. 32,
Issue. 9,
Wang, Lei
Sekimoto, Atsushi
Takehara, Yuto
Okano, Yasunori
Ujihara, Toru
and
Dost, Sadik
2020.
Optimal Control of SiC Crystal Growth in the RF-TSSG System Using Reinforcement Learning.
Crystals,
Vol. 10,
Issue. 9,
p.
791.
Tang, Hongwei
Rabault, Jean
Kuhnle, Alexander
Wang, Yan
and
Wang, Tongguang
2020.
Robust active flow control over a range of Reynolds numbers using an artificial neural network trained through deep reinforcement learning.
Physics of Fluids,
Vol. 32,
Issue. 5,
Shimomura, Satoshi
Sekimoto, Satoshi
Oyama, Akira
Fujii, Kozo
and
Nishida, Hiroyuki
2020.
Closed-Loop Flow Separation Control Using the Deep Q Network over Airfoil.
AIAA Journal,
Vol. 58,
Issue. 10,
p.
4260.
Fan, Dixia
Yang, Liu
Wang, Zhicheng
Triantafyllou, Michael S.
and
Karniadakis, George Em
2020.
Reinforcement learning for bluff body active flow control in experiments and simulations.
Proceedings of the National Academy of Sciences,
Vol. 117,
Issue. 42,
p.
26091.
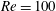 $Re=100$), our artificial neural network is able to learn an active control strategy from experimenting with the mass flow rates of two jets on the sides of a cylinder. By interacting with the unsteady wake, the artificial neural network successfully stabilizes the vortex alley and reduces drag by approximately 8 %. This is performed while using small mass flow rates for the actuation, of the order of 0.5 % of the mass flow rate intersecting the cylinder cross-section once a new pseudo-periodic shedding regime is found. This opens the way to a new class of methods for performing active flow control.
$Re=100$), our artificial neural network is able to learn an active control strategy from experimenting with the mass flow rates of two jets on the sides of a cylinder. By interacting with the unsteady wake, the artificial neural network successfully stabilizes the vortex alley and reduces drag by approximately 8 %. This is performed while using small mass flow rates for the actuation, of the order of 0.5 % of the mass flow rate intersecting the cylinder cross-section once a new pseudo-periodic shedding regime is found. This opens the way to a new class of methods for performing active flow control.
