Article contents
Analytical solutions for one-dimensional diabatic flows with wall friction
Published online by Cambridge University Press: 14 May 2021
Abstract
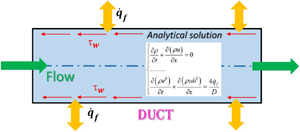
New analytical solutions for the one-dimensional (1-D) steady-state compressible viscous diabatic flow of an ideal gas through a constant cross-section pipe have been obtained. A constant and a variable heat flux with the walls, the latter being the more relevant for engineering applications, have been considered. To be able to analytically solve the problem, it is essential to determine the correct transformations of the variables and to identify the kinetic energy per unit of mass as the physical variable that appears in the final ordinary differential equation. A dimensionless representation of the analytical solutions, which points out the fundamental role exerted by a few dimensionless groups in problems where viscous power dissipation and heat transfer power are present simultaneously, is also presented. The obtained analytical solutions have successfully been validated for both subsonic and supersonic flows through a comparison with the corresponding numerical time asymptotic solutions of the generalised Euler equations for 1-D gas dynamics problems. The thus validated analytical solutions, which have also been physically discussed, extend Fanno's (1904) and Rayleigh's (1910) models that refer to 1-D steady-state viscous adiabatic and inviscid diabatic flows, respectively.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 9
- Cited by


