Hostname: page-component-7f64f4797f-8cpv7 Total loading time: 0 Render date: 2025-11-04T11:16:09.629Z Has data issue: false hasContentIssue false
  • English
  • Français

An asymptotic theory of the roughness impact on inviscid Mack modes in supersonic/hypersonic boundary layers

Published online by Cambridge University Press:  26 February 2021

Ming Dong Open the ORCID record for Ming Dong [Opens in a new window]  and
Lei Zhao
Ming Dong*
Affiliation:
Department of Mechanics, Tianjin University, Tianjin 300072, PR China
Lei Zhao
Affiliation:
Department of Mechanics, Tianjin University, Tianjin 300072, PR China
*
†Email address for correspondence: dongming@tju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

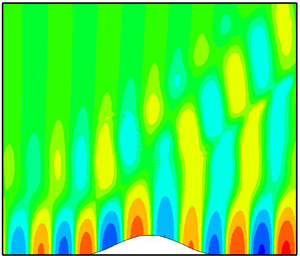
In this paper, we develop a large-Reynolds-number asymptotic theory to describe the impact of a localised roughness element on oncoming inviscid first and second Mack modes in supersonic or hypersonic boundary layers. The height and width of the roughness are assumed to be of $O(R^{-1/4}\delta ^{*})$ and $O(R^{1/4}\delta ^{*})$, respectively, such that the induced mean-flow distortion is described by the triple-deck formalism, where $R$ is the Reynolds number based on the local boundary-layer displacement thickness $\delta ^{*}$. As the wavelength of the inviscid Mack mode is comparable with $\delta ^{*}$, its interaction with the roughness forms a multi-scale problem. The Mack mode in the bulk of the boundary layer is described by the inviscid Rayleigh equation, whose evolution near the roughness is formulated by use of the solvability condition. It is found that the dominant roughness effect is attributed to both the interaction of the oncoming perturbation with the mean-flow distortion in the main layer and the inhomogeneous forcing from the curved wall (Stokes layer). This theory enables us to probe the scattering process when the frequency approaches the synchronisation frequency, which is recognised as the critical site distinguishing the destabilising and stabilising roles of the roughness. An improved asymptotic theory is also developed, which increases the accuracy of the asymptotic prediction, especially at the intersection frequency of the first and second modes. We also carry out harmonic linearised Navier–Stokes calculations and direct numerical simulations to confirm the accuracy of the asymptotic predictions, and favourable agreements are obtained even when the roughness height is a quarter of the nominal boundary-layer thickness.

JFM classification

Boundary Layers: Boundary layer stability Instability: Transition to turbulence

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A22
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Dong, M. 2020 Scattering of Tollmien–Schlichting waves by localized roughness in transonic boundary layers. Appl. Math. Mech. -Engl. Ed. 41, 1105–1124.CrossRefGoogle Scholar
Dong, M., Liu, Y. & Wu, X. 2020 Receptivity of inviscid modes in supersonic boundary layers due to scattering of freestream sound by wall roughness. J. Fluid Mech. 896, A23.CrossRefGoogle Scholar
Dong, M. & Zhang, A. 2018 Scattering of Tollmien–Schlichting waves as they pass over forward-/backward-facing steps. Appl. Math. Mech. -Engl. Ed. 39, 1411–1424.CrossRefGoogle Scholar
Duan, L., Wang, X. & Zhong, X. 2013 Stabilization of a Mach 5.92 boundary layer by two-dimensional finite-height roughness. AIAA J. 51, 266–270.CrossRefGoogle Scholar
Fedorov, A.V. 2003 a Receptivity of a high-speed boundary layer to acoustic disturbances. J. Fluid Mech. 491, 101–129.CrossRefGoogle Scholar
Fedorov, A.V. 2003 b Receptivity of hypersonic boundary layer to acoustic disturbances scattered by surface roughness. AIAA Paper 2003-3731.CrossRefGoogle Scholar
Fedorov, A.V 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–95.CrossRefGoogle Scholar
Fedorov, A.V. & Khokhlov, A.P. 1991 Excitation of unstable modes in a supersonic boundary layer by acoustic waves. Fluid Dyn. 9, 456–467.Google Scholar
Fedorov, A.V. & Khokhlov, A.P. 2001 Prehistory of instability in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 14, 359–375.CrossRefGoogle Scholar
Fedorov, A.V. & Khokhlov, A.P. 2002 Receptivity of hypersonic boundary layer to wall disturbances. Theor. Comput. Fluid Dyn. 15, 231–254.CrossRefGoogle Scholar
Fong, K., Wang, X., Huang, Y., Zhong, X., McKiernan, G., Figher, R. & Schneider, S. 2015 a Second mode suppression in hypersonic boundary layer by roughness: design and experiments. AIAA J. 53, 3138–3144.CrossRefGoogle Scholar
Fong, K., Wang, X. & Zhong, X. 2014 Numerical simulation of roughness effect on the stability of a hypersonic boundary layer. Comput. Fluids 96, 350–367.CrossRefGoogle Scholar
Fong, K., Wang, X. & Zhong, X. 2015 b Parametric study on stabilization of hypersonic boundray-layer waves using 2-D surface roughness. AIAA Paper 2015-0837.CrossRefGoogle Scholar
Fujii, K. 2006 Experiment of two-dimensional roughness effect on hypersonic boundary-layer transition. J. Spacecr. Rockets 43, 731–738.CrossRefGoogle Scholar
Goldstein, M.E. 1983 The evolution of Tollmien–Schlichting waves near a leading edge. J. Fluid Mech. 127, 59–81.CrossRefGoogle Scholar
Goldstein, M.E. 1985 Scattering of acoustic waves into Tollmien–Schlichting waves by small streamwise variations in surface geometry. J. Fluid Mech. 154, 509–530.CrossRefGoogle Scholar
Goldstein, M.E. & Ricco, P. 2018 Non-localized boundary layer instabilities resulting from leading edge receptivity at moderate supersonic Mach numbers. J. Fluid Mech. 838, 435–477.CrossRefGoogle Scholar
Hernández, C.G. & Wu, X. 2019 Receptivity of supersonic boundary layers over smooth and wavy surfaces to impinging slow acoustic waves. J. Fluid Mech. 872, 849–888.CrossRefGoogle Scholar
Holloway, P.F. & Sterrett, J.R. 1964 Effect of controlled surface roughness on boundary-layer transition and heat transfer at Mach numbers of 4.8 and 6.0. NASA TN D-2054.CrossRefGoogle Scholar
Jaffe, N.A., Okamura, T.T. & Smith, A.M.O. 1970 Determination of spatial amplification factors and their application to predicting transition. AIAA J. 8, 301–308.CrossRefGoogle Scholar
Kachanov, Y.S. 1994 Physical mechanisms of laminar-boundary-layer transition. Annu. Rev. Fluid Mech. 26, 411–482.CrossRefGoogle Scholar
Lees, L. & Lin, C.C. 1946 Investigation of the stability of the laminar boundary layer in a compressible fluid. Tech. Rep. 1115. NASA Tech. Note.Google Scholar
Liu, Y., Dong, M. & Wu, X. 2020 Generation of first Mack modes in supersonic boundary layers by slow acoustic waves interacting with streamwise isolated wall roughness. J. Fluid Mech. 888, A10.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2003 a Receptivity of a supersonic boundary layer over a flat plate. Part 1. Receptivity to free-stream sound. J. Fluid Mech. 488, 31–78.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2003 b Receptivity of a supersonic boundary layer over a flat plate. Part 2. Receptivity to freestream sound. J. Fluid Mech. 488, 79–121.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2005 Receptivity of a supersonic boundary layer over a flat plate. Part 3. Effects of different types of free-stream disturbances. J. Fluid Mech. 532, 63–109.CrossRefGoogle Scholar
Mack, L. 1987 Review of linear compressible stability theory. In Stability of Time Dependent and Spatially Varying Flows (ed. D.L. Dwoyer & M.Y. Hussaini), pp. 164–187. Springer.CrossRefGoogle Scholar
Malik, M. 1990 Finite difference solution of the compressible stability eigenvalue problem. NASA Tech. Rep. 16572, 86, 376–413.Google Scholar
Marxen, O., Iaccarino, G. & Shaqfeh, E. 2010 Disturbance evolution in a Mach 4.8 boundary layer with two-dimensional roughness-induced separation and shock. J. Fluid Mech. 648, 435–469.CrossRefGoogle Scholar
Maslov, A.A., Shiplyuk, A.N., Sidorenko, A.A. & Arnal, D. 2001 Leading-edge receptivity of a hypersonic boundary layer on a flat plate. J. Fluid Mech. 426, 73–94.CrossRefGoogle Scholar
Mengaldo, G., Kravtsova, M., Ruban, A.I. & Sherwin, S.J. 2015 Triple-deck and direct numerical simulation analyses of high-speed subsonic flows past a roughness element. J. Fluid Mech 774, 311–323.CrossRefGoogle Scholar
Messiter, A.F. 1970 Boundary layer flow near the trailing edge on a flat plate. SIAM J. Appl. Maths 18, 241–257.CrossRefGoogle Scholar
Park, D. & Park, S.O. 2013 Influence of two-dimensional smooth humps on linear and non-linear instability of a supersonic boundary layer. Comput. FLuids 30, 543–563.Google Scholar
Park, D. & Park, S.O. 2016 Study of effect of a smooth hump on hypersonic boundary layer instability. Theor. Comput. Fluid Dyn. 30, 543–563.CrossRefGoogle Scholar
Qin, H. & Dong, M 2016 Boundary-layer disturbances subjected to free-stream turbulence and simulation on bypass transition. Appl. Math. Mech. -Engl. Ed. 37, 967–986.CrossRefGoogle Scholar
Ricco, P. & Wu, X. 2007 Response of a compressible laminar boundary layer to free-stream vortical disturbances. J. Fluid Mech. 587, 97–138.CrossRefGoogle Scholar
Ruban, A.I. 1984 On Tollimien–Schlichting wave generation by sound (in Russian). Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza, No. 5, 44–52 (translation in Fluid Dyn. 19, 709–716).CrossRefGoogle Scholar
Ruban, A.I., Bernots, T. & Kravtsova, M.A. 2016 Linear and nonlinear receptivity of the boudnary layer in transonic flows. J. Fluid Mech. 786, 154–189.CrossRefGoogle Scholar
Schneider, S. 2008 Summary of hypersonic boundary-layer transition experiments on blunt bodies with roughness. J. Spacecr. Rockets 45, 1090–1105.CrossRefGoogle Scholar
Smith, A.M.O. 1956 Transition, pressure gradient and stability theory. In IX International Congress of Applied Mechanics, Brussels (ed. I.A.H. Hult & F.A. McClintocle).Google Scholar
Smith, F.T. 1973 Laminar flow over a small hump on flat plate. J. Fluid Mech. 57, 803–824.CrossRefGoogle Scholar
Smith, F.T. 1989 On the first-mode instability in subsonic, supersonic or hypersonic boundary layers. J. Fluid Mech. 198, 127–153.CrossRefGoogle Scholar
Smith, F.T., Brighton, P., Jackson, P. & Hunt, J. 1981 On boundary-layer flow past two-dimensional obstacles. J. Fluid Mech. 113, 123–152.CrossRefGoogle Scholar
Stewartson, K. 1969 On the flow near the trailing edge of a flat plate. Mathematika 16, 106–121.CrossRefGoogle Scholar
Tumin, A. 2007 Three-dimensional spatial normal modes in compressible boundary layers. J. Fluid Mech. 586, 295–322.CrossRefGoogle Scholar
Tumin, A.M. & Fedorov, A.V. 1983 Spatial growth of disturbances in a compressible boundary layer. J. Appl. Mech. Tech. Phys. 24, 548–554.CrossRefGoogle Scholar
Wu, X. 1999 Generation of Tollmien–Schlichting waves by convecting gusts interacting with sound. J. Fluid Mech. 397, 285–316.CrossRefGoogle Scholar
Wu, X. 2019 Nonlinear theories for shear flow instabilities: physical insights and practical implications. Annu. Rev. Fluid Mech. 51, 451–485.CrossRefGoogle Scholar
Wu, X. & Dong, M. 2016 a Entrainment of short-wavelength free-stream vortical disturbances in compressible and incompressible boundary layers. J. Fluid Mech. 797, 683–782.CrossRefGoogle Scholar
Wu, X. & Dong, M. 2016 b A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition: transmission coefficient as an eigenvalue. J. Fluid Mech. 794, 68–108.CrossRefGoogle Scholar
Zhao, L. & Dong, M. 2020 Effect of suction on laminar-flow control in subsonic boundary layers with forward-/backward-facing steps. Phys. Fluids 32, 054108.Google Scholar
Zhao, L., Dong, M. & Yang, Y. 2019 Harmonic linearized Navier–Stokes equation on describing the effect of surface roughness on hypersonic boundary-layer transition. Phys. Fluids 31, 034108.Google Scholar
Zhong, X. & Wang, X. 2012 Direct numerical simulation on the receptivity, instability and transition of hypersonic boundary layers. Annu. Rev. Fluid Mech. 44, 527–561.CrossRefGoogle Scholar