Article contents
Aero-optics of subsonic turbulent boundary layers
Published online by Cambridge University Press: 24 February 2012
Abstract
Compressible large-eddy simulations are carried out to study the aero-optical distortions caused by Mach 0.5 flat-plate turbulent boundary layers at Reynolds numbers of 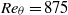 , 1770 and 3550, based on momentum thickness. The fluctuations of refractive index are calculated from the density field, and wavefront distortions of an optical beam traversing the boundary layer are computed based on geometric optics. The effects of aperture size, small-scale turbulence, different flow regions and beam elevation angle are examined and the underlying flow physics is analysed. It is found that the level of optical distortion decreases with increasing Reynolds number within the Reynolds-number range considered. The contributions from the viscous sublayer and buffer layer are small, while the wake region plays a dominant role, followed by the logarithmic layer. By low-pass filtering the fluctuating density field, it is shown that small-scale turbulence is optically inactive. Consistent with previous experimental findings, the distortion magnitude is dependent on the propagation direction due to anisotropy of the boundary-layer vortical structures. Density correlations and length scales are analysed to understand the elevation-angle dependence and its relation to turbulence structures. The applicability of Sutton’s linking equation to boundary-layer flows is examined, and excellent agreement between linking equation predictions and directly integrated distortions is obtained when the density length scale is appropriately defined.
, 1770 and 3550, based on momentum thickness. The fluctuations of refractive index are calculated from the density field, and wavefront distortions of an optical beam traversing the boundary layer are computed based on geometric optics. The effects of aperture size, small-scale turbulence, different flow regions and beam elevation angle are examined and the underlying flow physics is analysed. It is found that the level of optical distortion decreases with increasing Reynolds number within the Reynolds-number range considered. The contributions from the viscous sublayer and buffer layer are small, while the wake region plays a dominant role, followed by the logarithmic layer. By low-pass filtering the fluctuating density field, it is shown that small-scale turbulence is optically inactive. Consistent with previous experimental findings, the distortion magnitude is dependent on the propagation direction due to anisotropy of the boundary-layer vortical structures. Density correlations and length scales are analysed to understand the elevation-angle dependence and its relation to turbulence structures. The applicability of Sutton’s linking equation to boundary-layer flows is examined, and excellent agreement between linking equation predictions and directly integrated distortions is obtained when the density length scale is appropriately defined.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 106
- Cited by

