Article contents
Advection and buoyancy-induced turbulent mixing in a narrow vertical tank
Published online by Cambridge University Press: 29 April 2013
Abstract
We describe new experiments to examine the buoyancy-induced turbulent mixing which results from the injection of a small constant volume flux of dense fluid at the top of a long narrow vertical tank with square cross-section, in which a steady laminar upward flow of less dense fluid is present. To conserve volume of fluid in the tank, fluid leaves the tank through two small openings near the top of the tank. Dense source fluid vigorously mixes with the less dense fluid of the upward flow, such that a dense mixing region of turbulent fluid propagates downwards during the transient mixing phase of the experiment. Eventually, the transport of dense fluid associated with the buoyancy-induced turbulent flow is balanced by the transport of less-dense fluid associated with the steady upward flow, such that the mixing region evolves into a layer of finite extent which stays approximately constant in height during a statistically steady mixing phase of the experiment. With an ideal source of downward constant buoyancy flux 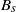 ${B}_{s} $ at the top of the tank, tank width
${B}_{s} $ at the top of the tank, tank width 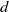 $d$ , and speed of the upward flow
$d$ , and speed of the upward flow 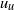 ${u}_{u} $ , we perform experiments with Froude numbers
${u}_{u} $ , we perform experiments with Froude numbers 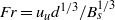 $\mathit{Fr}= {u}_{u} {d}^{1/ 3} / { B}_{s}^{1/ 3} $ ranging between
$\mathit{Fr}= {u}_{u} {d}^{1/ 3} / { B}_{s}^{1/ 3} $ ranging between 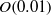 $O(0. 01)$ and
$O(0. 01)$ and 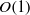 $O(1)$ . The steady-state height of the mixing region and the maximum reduced gravity as found near the source of buoyancy flux at the top of the tank increase with decreasing Froude number. For the experiments with intermediate values of the Froude number, we find that the steady-state mixing region is small enough to be contained in the experimental tank, but large enough not to be dominated by developing turbulence near the source of buoyancy flux. For these experiments, we show that the key buoyancy-induced turbulent mixing properties are not significantly affected by the upward flow. We use a dye-attenuation technique to obtain vertical profiles of the time- and horizontally averaged reduced gravity to show a good agreement between the experimental profiles and the solution of a nonlinear turbulent advection–diffusion equation during the steady mixing phase. Furthermore, we discuss the characteristic time scale of the transient mixing phase. We compare our experimental results with the numerical solution of a time-dependent nonlinear turbulent advection–diffusion equation during the transient mixing phase. We also describe three reduced models for the evolution of the reduced gravity distribution in the mixing region, and we demonstrate these models’ usefulness by comparison with our experimental results and the numerical solution of the time-dependent nonlinear turbulent advection–diffusion equation.
$O(1)$ . The steady-state height of the mixing region and the maximum reduced gravity as found near the source of buoyancy flux at the top of the tank increase with decreasing Froude number. For the experiments with intermediate values of the Froude number, we find that the steady-state mixing region is small enough to be contained in the experimental tank, but large enough not to be dominated by developing turbulence near the source of buoyancy flux. For these experiments, we show that the key buoyancy-induced turbulent mixing properties are not significantly affected by the upward flow. We use a dye-attenuation technique to obtain vertical profiles of the time- and horizontally averaged reduced gravity to show a good agreement between the experimental profiles and the solution of a nonlinear turbulent advection–diffusion equation during the steady mixing phase. Furthermore, we discuss the characteristic time scale of the transient mixing phase. We compare our experimental results with the numerical solution of a time-dependent nonlinear turbulent advection–diffusion equation during the transient mixing phase. We also describe three reduced models for the evolution of the reduced gravity distribution in the mixing region, and we demonstrate these models’ usefulness by comparison with our experimental results and the numerical solution of the time-dependent nonlinear turbulent advection–diffusion equation.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 7
- Cited by

