Article contents
Acoustic streaming in Maxwell fluids generated by standing waves in two-dimensional microchannels
Published online by Cambridge University Press: 06 January 2022
Abstract
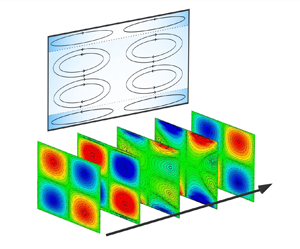
In this work, a semianalytic solution for the acoustic streaming phenomenon, generated by standing waves in Maxwell fluids through a two-dimensional microchannel (resonator), is derived. The mathematical model is non-dimensionalized and several dimensionless parameters that characterize the phenomenon arise: the ratio between the oscillation amplitude of the resonator and the half-wavelength ( $\eta =2A/\lambda _{a}$); the product of the fluid relaxation time times the angular frequency known as the Deborah number (
$\eta =2A/\lambda _{a}$); the product of the fluid relaxation time times the angular frequency known as the Deborah number ( $De=\lambda _{1}\omega$); the aspect ratio between the microchannel height and the wavelength (
$De=\lambda _{1}\omega$); the aspect ratio between the microchannel height and the wavelength ( $\epsilon =2 H_{0}/\lambda _{a}$); and the ratio between half the height of the microchannel and the thickness of the viscous boundary layer (
$\epsilon =2 H_{0}/\lambda _{a}$); and the ratio between half the height of the microchannel and the thickness of the viscous boundary layer ( $\alpha =H_{0}/\delta _{\nu }$). In the limit when
$\alpha =H_{0}/\delta _{\nu }$). In the limit when  $\eta \ll 1$, we obtain the hydrodynamic behaviour of the system using a regular perturbation method. In the present work, we show that the acoustic streaming speed is proportional to
$\eta \ll 1$, we obtain the hydrodynamic behaviour of the system using a regular perturbation method. In the present work, we show that the acoustic streaming speed is proportional to  $\alpha ^{2.65}De^{1.9}$, and the acoustic pressure varies as
$\alpha ^{2.65}De^{1.9}$, and the acoustic pressure varies as  $\alpha ^{6/5}De^{1/2}$. Also, we have found that the growth of inner vortex is due to convective terms in the Maxwell rheological equation. Furthermore, the velocity antinodes show a high dependency on the Deborah number, highlighting the fluid's viscoelastic properties and the appearance of resonance points. Due to the limitations of perturbation methods, we will only analyse narrow microchannels.
$\alpha ^{6/5}De^{1/2}$. Also, we have found that the growth of inner vortex is due to convective terms in the Maxwell rheological equation. Furthermore, the velocity antinodes show a high dependency on the Deborah number, highlighting the fluid's viscoelastic properties and the appearance of resonance points. Due to the limitations of perturbation methods, we will only analyse narrow microchannels.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 2
- Cited by


