Article contents
Acceleration in turbulent channel flow: universalities in statistics, subgrid stochastic models and an application
Published online by Cambridge University Press: 21 March 2013
Abstract
This paper focuses on the characterization and the stochastic modelling of the fluid acceleration in turbulent channel flow. In the first part, the acceleration is studied by direct numerical simulation (DNS) at three Reynolds numbers ( 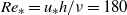 ${\mathit{Re}}_{\ast } = {u}_{\ast } h/ \nu = 180$ , 590 and 1000). It is observed that whatever the wall distance is, the norm of acceleration is log-normally distributed and that the variance of the norm is very close to its mean value. It is also observed that from the wall to the centreline of the channel, the orientation of acceleration relaxes statistically towards isotropy. On the basis of dimensional analysis, a universal scaling law for the acceleration norm is proposed. In the second part, in the framework of the norm/orientation decomposition, a stochastic model of the acceleration is introduced. The stochastic model for the norm is based on fragmentation process which evolves across the channel with the wall distance. Simultaneously the orientation is simulated by a random walk on the surface of a unit sphere. The process is generated in such a way that the mean components of the orientation vector are equal to zero, whereas with increasing wall distance, all directions become equally probable. In the third part, the models are assessed in the framework of large-eddy simulation with stochastic subgrid acceleration model (LES–SSAM), introduced recently by Sabel’nikov, Chtab-Desportes & Gorokhovski (Euro. Phys. J. B, vol. 80, 2011, p. 177–187), and designed to account for the intermittency at subgrid scales. Computations by LES–SSAM and its assessment using DNS data show that the prediction of important statistics to characterize the flow, such as the mean velocity, the energy spectra at small scales, the viscous and turbulent stresses, the distribution of the acceleration can be considerably improved in comparison with standard LES. In the last part of this paper, the advantage of LES–SSAM in accounting for the subgrid flow structure is demonstrated in simulation of particle-laden turbulent channel flows. Compared to standard LES, it is shown that for different Stokes numbers, the particle dynamics and the turbophoresis effect can be predicted significantly better when LES–SSAM is applied.
${\mathit{Re}}_{\ast } = {u}_{\ast } h/ \nu = 180$ , 590 and 1000). It is observed that whatever the wall distance is, the norm of acceleration is log-normally distributed and that the variance of the norm is very close to its mean value. It is also observed that from the wall to the centreline of the channel, the orientation of acceleration relaxes statistically towards isotropy. On the basis of dimensional analysis, a universal scaling law for the acceleration norm is proposed. In the second part, in the framework of the norm/orientation decomposition, a stochastic model of the acceleration is introduced. The stochastic model for the norm is based on fragmentation process which evolves across the channel with the wall distance. Simultaneously the orientation is simulated by a random walk on the surface of a unit sphere. The process is generated in such a way that the mean components of the orientation vector are equal to zero, whereas with increasing wall distance, all directions become equally probable. In the third part, the models are assessed in the framework of large-eddy simulation with stochastic subgrid acceleration model (LES–SSAM), introduced recently by Sabel’nikov, Chtab-Desportes & Gorokhovski (Euro. Phys. J. B, vol. 80, 2011, p. 177–187), and designed to account for the intermittency at subgrid scales. Computations by LES–SSAM and its assessment using DNS data show that the prediction of important statistics to characterize the flow, such as the mean velocity, the energy spectra at small scales, the viscous and turbulent stresses, the distribution of the acceleration can be considerably improved in comparison with standard LES. In the last part of this paper, the advantage of LES–SSAM in accounting for the subgrid flow structure is demonstrated in simulation of particle-laden turbulent channel flows. Compared to standard LES, it is shown that for different Stokes numbers, the particle dynamics and the turbophoresis effect can be predicted significantly better when LES–SSAM is applied.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
Footnotes
Present address: Center for Turbulence Research, Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA.
References
- 23
- Cited by

