Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wong, Jaime G.
and
Rival, David E.
2014.
Exploring Vortex Stability on Two-Dimensional Rotating Plates with Varying Sweepback.
Wolfinger, M.
and
Rockwell, D.
2014.
Flow structure on a rotating wing: effect of radius of gyration.
Journal of Fluid Mechanics,
Vol. 755,
Issue. ,
p.
83.
Manar, Field
Medina, Albert
and
Jones, Anya R.
2014.
Tip vortex structure and aerodynamic loading on rotating wings in confined spaces.
Experiments in Fluids,
Vol. 55,
Issue. 9,
Limacher, Eric J.
and
Rival, David E.
2014.
On the Stable Leading Edge Vortex in Rotating Systems.
Li, Juan
and
Wu, Zi-Niu
2015.
Unsteady lift for the Wagner problem in the presence of additional leading/trailing edge vortices.
Journal of Fluid Mechanics,
Vol. 769,
Issue. ,
p.
182.
Carr, Zakery R.
DeVoria, Adam C.
and
Ringuette, Matthew J.
2015.
Aspect-ratio effects on rotating wings: circulation and forces.
Journal of Fluid Mechanics,
Vol. 767,
Issue. ,
p.
497.
Eslam Panah, Azar
Akkala, James M.
and
Buchholz, James H. J.
2015.
Vorticity transport and the leading-edge vortex of a plunging airfoil.
Experiments in Fluids,
Vol. 56,
Issue. 8,
Wong, Jaime G.
and
Rival, David E.
2015.
Determining the relative stability of leading-edge vortices on nominally two-dimensional flapping profiles.
Journal of Fluid Mechanics,
Vol. 766,
Issue. ,
p.
611.
Manar, Field H.
Mancini, Peter
and
Jones, Anya R.
2015.
Vortex Characterization and Force Production on Two- and Three-Dimensional Wing Kinematics.
Bross, M.
and
Rockwell, D.
2015.
Three-dimensional flow structure along simultaneously pitching and rotating wings: effect of pitch rate.
Experiments in Fluids,
Vol. 56,
Issue. 4,
Widmann, A.
and
Tropea, C.
2015.
Parameters influencing vortex growth and detachment on unsteady aerodynamic profiles.
Journal of Fluid Mechanics,
Vol. 773,
Issue. ,
p.
432.
Limacher, Eric
and
Rival, David E.
2015.
On the distribution of leading-edge vortex circulation in samara-like flight.
Journal of Fluid Mechanics,
Vol. 776,
Issue. ,
p.
316.
Medina, Albert
and
Jones, Anya R.
2015.
Stereoscopic PIV analysis on rotary plates in bursting.
Onoue, Kyohei
Song, Arnold
Strom, Benjamin
and
Breuer, Kenneth S.
2015.
Large amplitude flow-induced oscillations and energy harvesting using a cyber-physical pitching plate.
Journal of Fluids and Structures,
Vol. 55,
Issue. ,
p.
262.
Limacher, Eric
Morton, Chris
and
Wood, David
2016.
On the trajectory of leading-edge vortices under the influence of Coriolis acceleration.
Journal of Fluid Mechanics,
Vol. 800,
Issue. ,
Chintamani, Siddarth
Rege, Alok A.
Dennis, Brian H.
and
Subbarao, Kamesh
2016.
Three-dimensional Effects in the Wake Vortex Formation of Flapping Flat Plate in Hover.
Medina, Albert
and
Jones, Anya R.
2016.
Leading-edge vortex burst on a low-aspect-ratio rotating flat plate.
Physical Review Fluids,
Vol. 1,
Issue. 4,
Manar, Field
Mancini, Peter
Mayo, David
and
Jones, Anya R.
2016.
Comparison of Rotating and Translating Wings: Force Production and Vortex Characteristics.
AIAA Journal,
Vol. 54,
Issue. 2,
p.
519.
Bottom II, R. G.
Borazjani, I.
Blevins, E. L.
and
Lauder, G. V.
2016.
Hydrodynamics of swimming in stingrays: numerical simulations and the role of the leading-edge vortex.
Journal of Fluid Mechanics,
Vol. 788,
Issue. ,
p.
407.
Akkala, James
and
Buchholz, James
2016.
The Role of Vorticity Transport in the Detachment of Unsteady Leading-Edge Vortices.
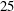 $25$ and
$25$ and 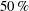 $50\, \%$ spanwise positions suggests that, although spanwise velocity is significant, spanwise convection of vorticity is insufficient to balance the flux of vorticity from the leading-edge shear layer. Subsequent detailed analyses of vorticity transport in planar control volumes at the
$50\, \%$ spanwise positions suggests that, although spanwise velocity is significant, spanwise convection of vorticity is insufficient to balance the flux of vorticity from the leading-edge shear layer. Subsequent detailed analyses of vorticity transport in planar control volumes at the 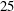 $25$ and
$25$ and 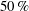 $50\, \%$ spanwise positions verify this conclusion and demonstrate that vorticity annihilation due to interaction between the leading-edge vortex and the opposite-sign layer on the plate surface is an important, often dominant, mechanism for regulation of leading-edge-vortex circulation. Thus, it provides an important condition for maintenance of an attached leading-edge vortex on the inboard portion of the blade.
$50\, \%$ spanwise positions verify this conclusion and demonstrate that vorticity annihilation due to interaction between the leading-edge vortex and the opposite-sign layer on the plate surface is an important, often dominant, mechanism for regulation of leading-edge-vortex circulation. Thus, it provides an important condition for maintenance of an attached leading-edge vortex on the inboard portion of the blade.
