Article contents
Vapour-bubble nucleation and dynamics in turbulent Rayleigh–Bénard convection
Published online by Cambridge University Press: 13 April 2016
Abstract
Vapour bubbles nucleating at micro-cavities etched into the silicon bottom plate of a cylindrical Rayleigh–Bénard sample (diameter  $D=8.8$ cm, aspect ratio
$D=8.8$ cm, aspect ratio 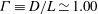 ${\it\Gamma}\equiv D/L\simeq 1.00$ where
${\it\Gamma}\equiv D/L\simeq 1.00$ where 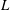 $L$ is the sample height) were visualized from the top and from the side. A triangular array of cylindrical micro-cavities (with a diameter of
$L$ is the sample height) were visualized from the top and from the side. A triangular array of cylindrical micro-cavities (with a diameter of 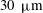 $30~{\rm\mu}\text{m}$ and a depth of
$30~{\rm\mu}\text{m}$ and a depth of 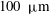 $100~{\rm\mu}\text{m}$ ) covered a circular centred area (diameter of 2.5 cm) of the bottom plate. Heat was applied to the sample only over this central area while cooling was over the entire top-plate area. Bubble sizes and frequencies of departure from the bottom plate are reported for a range of bottom-plate superheats
$100~{\rm\mu}\text{m}$ ) covered a circular centred area (diameter of 2.5 cm) of the bottom plate. Heat was applied to the sample only over this central area while cooling was over the entire top-plate area. Bubble sizes and frequencies of departure from the bottom plate are reported for a range of bottom-plate superheats 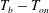 $T_{b}-T_{on}$ (
$T_{b}-T_{on}$ ( 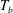 $T_{b}$ is the bottom-plate temperature,
$T_{b}$ is the bottom-plate temperature, 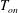 $T_{on}$ is the onset temperature of bubble nucleation) from 3 to 12 K for three different cavity separations. The difference
$T_{on}$ is the onset temperature of bubble nucleation) from 3 to 12 K for three different cavity separations. The difference  $T_{b}-T_{t}\simeq 16$ K between
$T_{b}-T_{t}\simeq 16$ K between 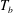 $T_{b}$ and the top plate temperature
$T_{b}$ and the top plate temperature 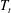 $T_{t}$ was kept fixed while the mean temperature
$T_{t}$ was kept fixed while the mean temperature 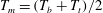 $T_{m}=(T_{b}+T_{t})/2$ was varied, leading to a small range of the Rayleigh number
$T_{m}=(T_{b}+T_{t})/2$ was varied, leading to a small range of the Rayleigh number 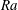 $Ra$ from
$Ra$ from 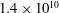 $1.4\times 10^{10}$ to
$1.4\times 10^{10}$ to 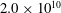 $2.0\times 10^{10}$ . The time between bubble departures from a given cavity decreased exponentially with increasing superheat and was independent of cavity separation. The contribution of the bubble latent heat to the total enhancement of heat transferred due to bubble nucleation was found to increase with superheat, reaching up to 25 %. The bubbly flow was examined in greater detail for a superheat of 10 K and
$2.0\times 10^{10}$ . The time between bubble departures from a given cavity decreased exponentially with increasing superheat and was independent of cavity separation. The contribution of the bubble latent heat to the total enhancement of heat transferred due to bubble nucleation was found to increase with superheat, reaching up to 25 %. The bubbly flow was examined in greater detail for a superheat of 10 K and 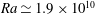 $Ra\simeq 1.9\times 10^{10}$ . The condensation and/or dissolution rates of departed bubbles revealed two regimes: the initial rate was influenced by steep thermal gradients across the thermal boundary layer near the plate and was two orders of magnitude larger than the final condensation and/or dissolution rate that prevailed once the rising bubbles were in the colder bulk flow of nearly uniform temperature. The dynamics of thermal plumes was studied qualitatively in the presence and absence of nucleating bubbles. It was found that bubbles enhanced the plume velocity by a factor of four or so and drove a large-scale circulation (LSC). Nonetheless, even in the presence of bubbles the plumes and LSC had a characteristic velocity which was smaller by a factor of five or so than the bubble-rise velocity in the bulk. In the absence of bubbles there was strongly turbulent convection but no LSC, and plumes on average rose vertically.
$Ra\simeq 1.9\times 10^{10}$ . The condensation and/or dissolution rates of departed bubbles revealed two regimes: the initial rate was influenced by steep thermal gradients across the thermal boundary layer near the plate and was two orders of magnitude larger than the final condensation and/or dissolution rate that prevailed once the rising bubbles were in the colder bulk flow of nearly uniform temperature. The dynamics of thermal plumes was studied qualitatively in the presence and absence of nucleating bubbles. It was found that bubbles enhanced the plume velocity by a factor of four or so and drove a large-scale circulation (LSC). Nonetheless, even in the presence of bubbles the plumes and LSC had a characteristic velocity which was smaller by a factor of five or so than the bubble-rise velocity in the bulk. In the absence of bubbles there was strongly turbulent convection but no LSC, and plumes on average rose vertically.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
Narezo Guzman et al. supplementary movie
Movie from which figure 5(a) was extracted. The movie shows the bubble detachment process from the bottom plate with superheat of about 10 K and a cavity separation of 0.6 mm. The movie was recorded at 500 frames per second and was slowed down 20 times for display.
Narezo Guzman et al. supplementary movie
Movie from which figure 5(b) was extracted. The movie shows the detached bubbles rising across 0.4 of the cell height. The bottom plate superheat was about 10 K and the cavity separation was 0.6 mm. The movie was recorded at 1000 frames per second and was slowed down 40 times for display.
Narezo Guzman et al. supplementary movie
Shadowgraph visualization of two-phase flow capturing the entire cell between bottom to top plates. Movie from which figure 6(a) was extracted. Movie is displayed in real time. The bottom plate superheat was about 10 K and the cavity separation was 0.6 mm.
Narezo Guzman et al. supplementary movie
Shadowgraph visualization of one-phase flow capturing the entire cell between bottom to top plates. Movie from which figure 6(b) was extracted. Movie is displayed in real time. The bottom plate superheat was about 10 K and the cavity separation was 0.6 mm.
Narezo Guzman et al. supplementary movie
Movie from which figure 8(d) was extracted. The movie shows bubbles detaching from the bottom plate and rising until eventually they fully condense and dissolve. The movie captured the flow between bottom and top plates and was recorded at 500 frames per second and slowed down 20 times for display. The bottom plate superheat was about 10 K and the cavity separation was 0.6 mm.
- 6
- Cited by


