Article contents
A two-dimensional-three-component model for spanwise rotating plane Poiseuille flow
Published online by Cambridge University Press: 09 October 2019
Abstract
Spanwise rotating plane Poiseuille flow (RPPF) is one of the canonical flow problems to study the effect of system rotation on wall-bounded shear flows and has been studied a lot in the past. In the present work, a two-dimensional-three-component (2D/3C) model for RPPF is introduced and it is shown that the present model is equivalent to a thermal convection problem with unit Prandtl number. For low Reynolds number cases, the model can be used to study the stability behaviour of the roll cells. It is found that the neutral stability curves, critical eigensolutions and critical streamfunctions of RPPF at different rotation numbers ( $Ro$) almost collapse with the help of a rescaling with a newly defined Rayleigh number
$Ro$) almost collapse with the help of a rescaling with a newly defined Rayleigh number 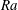 $Ra$ and channel height
$Ra$ and channel height 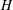 $H$. Analytic expressions for the critical Reynolds number and critical wavenumber at different
$H$. Analytic expressions for the critical Reynolds number and critical wavenumber at different 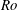 $Ro$ can be obtained. For a turbulent state with high Reynolds number, the 2D/3C model for RPPF is self-sustained even without extra excitations. Simulation results also show that the profiles of mean streamwise velocity and Reynolds shear stress from the 2D/3C model share the same linear laws as the fully three-dimensional cases, although differences on the intercepts can be observed. The contours of streamwise velocity fluctuations behave like plumes in the linear law region. We also provide an explanation to the linear mean velocity profiles observed at high rotation numbers.
$Ro$ can be obtained. For a turbulent state with high Reynolds number, the 2D/3C model for RPPF is self-sustained even without extra excitations. Simulation results also show that the profiles of mean streamwise velocity and Reynolds shear stress from the 2D/3C model share the same linear laws as the fully three-dimensional cases, although differences on the intercepts can be observed. The contours of streamwise velocity fluctuations behave like plumes in the linear law region. We also provide an explanation to the linear mean velocity profiles observed at high rotation numbers.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 7
- Cited by

