Article contents
Two-dimensional unsteadiness map of oblique shock wave/boundary layer interaction with sidewalls
Published online by Cambridge University Press: 24 May 2019
Abstract
The low-frequency unsteadiness of oblique shock wave/boundary layer interactions (SBLIs) has been investigated using large-eddy simulation (LES) and high-frequency pressure measurements from experiments. Particular attention has been paid to off-centreline behaviour: the LES dataset was generated including sidewalls, and experimental pressure measurements were acquired across the entire span of the reflected shock foot. The datasets constitute the first maps of low-frequency unsteadiness in both streamwise and spanwise directions. The results reveal that significant low-frequency shock motion (with 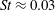 $St\approx 0.03$) occurs away from the centreline, along most of the central separation shock and in the corner regions. The most powerful low-frequency unsteadiness occurs off-centre, likely due to the separation shock being strengthened by shocks arising from the swept interactions on the sidewalls. Both simulation and experimental results exhibit asymmetry about the spanwise centre. In simulations, this may be attributed to a lack of statistical convergence; however, the fact that this is also seen in experiments is indicative that some SBLIs may exhibit some inherent asymmetry across the two spanwise halves of the separation bubble. There is also significant low-frequency power in the corner separations. The relation of the unsteadiness in the corner regions to that in the centre is investigated by means of two-point correlations: a key observation is that significant correlation does not extend across the attached flow channel between the central and corner separations.
$St\approx 0.03$) occurs away from the centreline, along most of the central separation shock and in the corner regions. The most powerful low-frequency unsteadiness occurs off-centre, likely due to the separation shock being strengthened by shocks arising from the swept interactions on the sidewalls. Both simulation and experimental results exhibit asymmetry about the spanwise centre. In simulations, this may be attributed to a lack of statistical convergence; however, the fact that this is also seen in experiments is indicative that some SBLIs may exhibit some inherent asymmetry across the two spanwise halves of the separation bubble. There is also significant low-frequency power in the corner separations. The relation of the unsteadiness in the corner regions to that in the centre is investigated by means of two-point correlations: a key observation is that significant correlation does not extend across the attached flow channel between the central and corner separations.
JFM classification
Information
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 19
- Cited by

