Article contents
Two-dimensional modelling of transient capillary driven damped micro-oscillations and self-alignment of objects in microassembly
Published online by Cambridge University Press: 08 January 2021
Abstract
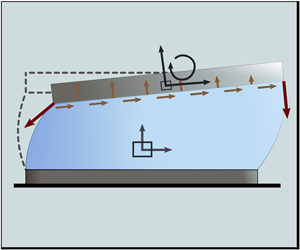
In the fields of microgripping and microassembly, the self-alignment motion of a solid micro-object linked by a liquid meniscus to a substrate or a tool is an inexpensive way to overcome the current limitations of the assembly processes at microscale by getting rid of the positioning actuators. Original models providing a dynamical description of the capillary self-alignment of an  $L\times D \times d$ chip are reported, as well as experimental results as evidence of their validity. The first two models describe the liquid and the solid physics in two dimensions. Both include nonlinearities and describe the coupling between a laminar flow and a solid structure. The fluid–solid coupling is ensured by the boundary conditions at their surface of contact and by the forces the liquid and the solid apply on each other. Both models yield the shift, lift and tilt modes of deformation of the liquid meniscus. Equations are first numerically solved by using a finite element method (model 1). By approximating the menisci with spherical caps, a geometrical model is then presented (model 2). Next, for small oscillations and thin liquid layers, the equations are linearised. The solution to the semianalytical three degrees of freedom (3-DOF) modal analysis is thus obtained (model 3). Finally, a semianalytical 1-DOF model is presented and numerically solved by considering a one-dimensional motion for the solid object (model 4). Solutions for models 1, 3 and 4 are computed and show good agreement with the experimental measurements. Yet, the remaining deviations are investigated to identify their origin.
$L\times D \times d$ chip are reported, as well as experimental results as evidence of their validity. The first two models describe the liquid and the solid physics in two dimensions. Both include nonlinearities and describe the coupling between a laminar flow and a solid structure. The fluid–solid coupling is ensured by the boundary conditions at their surface of contact and by the forces the liquid and the solid apply on each other. Both models yield the shift, lift and tilt modes of deformation of the liquid meniscus. Equations are first numerically solved by using a finite element method (model 1). By approximating the menisci with spherical caps, a geometrical model is then presented (model 2). Next, for small oscillations and thin liquid layers, the equations are linearised. The solution to the semianalytical three degrees of freedom (3-DOF) modal analysis is thus obtained (model 3). Finally, a semianalytical 1-DOF model is presented and numerically solved by considering a one-dimensional motion for the solid object (model 4). Solutions for models 1, 3 and 4 are computed and show good agreement with the experimental measurements. Yet, the remaining deviations are investigated to identify their origin.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 2
- Cited by


