Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Skote, Martin
2013.
Comparison between spatial and temporal wall oscillations in turbulent boundary layer flows.
Journal of Fluid Mechanics,
Vol. 730,
Issue. ,
p.
273.
Ricco, Pierre
and
Hahn, Stanislav
2013.
Control of Wall Turbulence by Spinning Discs.
Advanced Materials Research,
Vol. 745,
Issue. ,
p.
135.
Wise, Daniel J.
Alvarenga, Claudia
and
Ricco, Pierre
2014.
Spinning out of control: Wall turbulence over rotating discs.
Physics of Fluids,
Vol. 26,
Issue. 12,
Wise, Daniel J.
and
Ricco, Pierre
2014.
Turbulent drag reduction through oscillating discs.
Journal of Fluid Mechanics,
Vol. 746,
Issue. ,
p.
536.
Conlin, A.
and
Mao, X.
2015.
Suppression of force fluctuations in flow past an aerofoil.
International Journal of Computational Fluid Dynamics,
Vol. 29,
Issue. 6-8,
p.
325.
Hong, Cheng
Jang, Chun
and
Choi, Hyoung
2015.
Turbulent Drag Reduction with Polymers in Rotating Disk Flow.
Polymers,
Vol. 7,
Issue. 7,
p.
1279.
Ge, Mingwei
Zuo, Yingtao
Deng, Ying
and
Li, Yuhua
2015.
Spatial relation between fluctuating wall pressure and near-wall streamwise vortices in wall bounded turbulent flow.
Applied Mathematics and Mechanics,
Vol. 36,
Issue. 6,
p.
719.
Skote, Martin
Mishra, Maneesh
and
Wu, Yanhua
2015.
Drag Reduction of a Turbulent Boundary Layer over an Oscillating Wall and Its Variation with Reynolds Number.
International Journal of Aerospace Engineering,
Vol. 2015,
Issue. ,
p.
1.
Li, W.
Jessen, W.
Roggenkamp, D.
Klaas, M.
Silex, W.
Schiek, M.
and
Schröder, W.
2015.
Turbulent drag reduction by spanwise traveling ribbed surface waves.
European Journal of Mechanics - B/Fluids,
Vol. 53,
Issue. ,
p.
101.
Gatti, Davide
Güttler, Andreas
Frohnapfel, Bettina
and
Tropea, Cameron
2015.
Experimental assessment of spanwise-oscillating dielectric electroactive surfaces for turbulent drag reduction in an air channel flow.
Experiments in Fluids,
Vol. 56,
Issue. 5,
Khosh Aghdam, Sohrab
and
Ricco, Pierre
2016.
Laminar and turbulent flows over hydrophobic surfaces with shear-dependent slip length.
Physics of Fluids,
Vol. 28,
Issue. 3,
Meysonnat, Pascal S.
Roggenkamp, Dorothee
Li, Wenfeng
Roidl, Benedikt
and
Schröder, Wolfgang
2016.
Experimental and numerical investigation of transversal traveling surface waves for drag reduction.
European Journal of Mechanics - B/Fluids,
Vol. 55,
Issue. ,
p.
313.
Heins, Peter H.
Jones, Bryn Ll.
and
Sharma, Ati S.
2016.
Passivity-based output-feedback control of turbulent channel flow.
Automatica,
Vol. 69,
Issue. ,
p.
348.
Straub, Steffen
Vinuesa, Ricardo
Schlatter, Philipp
Frohnapfel, Bettina
and
Gatti, Davide
2017.
Turbulent Duct Flow Controlled with Spanwise Wall Oscillations.
Flow, Turbulence and Combustion,
Vol. 99,
Issue. 3-4,
p.
787.
Pyta, Lorenz
Meysonnat, Pascal S.
Schroder, Wolfgang
and
Abel, Dirk
2017.
Space-selective nonlinear reduced-order models for turbulent boundary layer drag reduction.
p.
383.
Han, Wen Jiao
and
Choi, Hyoung Jin
2017.
Role of Bio-Based Polymers on Improving Turbulent Flow Characteristics: Materials and Application.
Polymers,
Vol. 9,
Issue. 6,
p.
209.
Wise, Daniel J.
Olivucci, Paolo
and
Ricco, Pierre
2018.
Turbulent drag reduction through oscillating discs – CORRIGENDUM.
Journal of Fluid Mechanics,
Vol. 856,
Issue. ,
p.
1064.
Munday, Phillip M.
and
Taira, Kunihiko
2018.
Effects of Wall-Normal and Angular Momentum Injections in Airfoil Separation Control.
AIAA Journal,
Vol. 56,
Issue. 5,
p.
1830.
Abdulbari, Hayder A.
Salleh, Mohamad Amran Mohd
Rashed, Musaab K.
and
Ismail, M. Halim Shah
2018.
Passive, active, and interactive drag-reduction technique to reduce friction and enhance the mixing intensity in rotating disk apparatus.
Chemical Engineering Communications,
Vol. 205,
Issue. 12,
p.
1623.
Gatti, Davide
Stroh, Alexander
Frohnapfel, Bettina
and
Hasegawa, Yosuke
2018.
Predicting Turbulent Spectra in Drag-reduced Flows.
Flow, Turbulence and Combustion,
Vol. 100,
Issue. 4,
p.
1081.
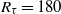 ${R}_{\tau } = 180$ , based on the friction velocity of the stationary-wall case and the half channel height. For a fixed maximum disc tip velocity, drag reduction can be achieved when the disc diameter is larger than a threshold, while below this threshold the drag increases. A maximum drag reduction of 23% is computed. The net power saved, obtained by taking into account the power spent to enforce the rotational motion against the fluid viscous resistance, is found to be positive and reach 10%. The disc-flow parameters required for commercial aircraft flight conditions and flows over high-speed trains and ship hulls are estimated and future implementations based on existing micro-electromagnetic motor and micro-air turbine technologies are discussed.
${R}_{\tau } = 180$ , based on the friction velocity of the stationary-wall case and the half channel height. For a fixed maximum disc tip velocity, drag reduction can be achieved when the disc diameter is larger than a threshold, while below this threshold the drag increases. A maximum drag reduction of 23% is computed. The net power saved, obtained by taking into account the power spent to enforce the rotational motion against the fluid viscous resistance, is found to be positive and reach 10%. The disc-flow parameters required for commercial aircraft flight conditions and flows over high-speed trains and ship hulls are estimated and future implementations based on existing micro-electromagnetic motor and micro-air turbine technologies are discussed.
