Article contents
Triggering turbulence efficiently in plane Couette flow
Published online by Cambridge University Press: 27 September 2012
Abstract
We use a variational formulation incorporating the full Navier–Stokes equations to identify initial perturbations with finite kinetic energy  ${E}_{0} $ which generate the largest gain in perturbation kinetic energy at some time
${E}_{0} $ which generate the largest gain in perturbation kinetic energy at some time 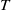 $T$ later for plane Couette flow. Using the flow geometry originally used by Butler & Farrell (Phys. Fluids A, vol. 4, 1992, pp. 1637–1650) to identify the linear transient optimal perturbations for
$T$ later for plane Couette flow. Using the flow geometry originally used by Butler & Farrell (Phys. Fluids A, vol. 4, 1992, pp. 1637–1650) to identify the linear transient optimal perturbations for 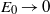 ${E}_{0} \ensuremath{\rightarrow} 0$ and incorporating
${E}_{0} \ensuremath{\rightarrow} 0$ and incorporating 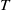 $T$ as part of the optimization procedure, we show how the addition of nonlinearity smoothly changes the result as
$T$ as part of the optimization procedure, we show how the addition of nonlinearity smoothly changes the result as 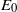 ${E}_{0} $ increases from zero until a small but finite
${E}_{0} $ increases from zero until a small but finite 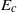 ${E}_{c} $ is reached. At this point, the variational algorithm is able to identify an initial condition of completely different form which triggers turbulence – called the minimal seed for turbulence. If instead
${E}_{c} $ is reached. At this point, the variational algorithm is able to identify an initial condition of completely different form which triggers turbulence – called the minimal seed for turbulence. If instead 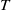 $T$ is fixed at some asymptotically large value, as suggested by Pringle, Willis & Kerswell (J. Fluid Mech., vol. 703, 2012, pp. 415–443), a fundamentally different ‘final’ optimal perturbation emerges from our algorithm above some threshold initial energy
$T$ is fixed at some asymptotically large value, as suggested by Pringle, Willis & Kerswell (J. Fluid Mech., vol. 703, 2012, pp. 415–443), a fundamentally different ‘final’ optimal perturbation emerges from our algorithm above some threshold initial energy 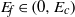 ${E}_{f} \in (0, {E}_{c} )$ which shows signs of localization. This nonlinear optimal perturbation clearly approaches the structure of the minimal seed as
${E}_{f} \in (0, {E}_{c} )$ which shows signs of localization. This nonlinear optimal perturbation clearly approaches the structure of the minimal seed as 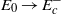 ${E}_{0} \ensuremath{\rightarrow} { E}_{c}^{\ensuremath{-} } $ , although for
${E}_{0} \ensuremath{\rightarrow} { E}_{c}^{\ensuremath{-} } $ , although for 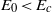 ${E}_{0} \lt {E}_{c} $ , its maximum gain over all time intervals is always less than the equivalent maximum gain for the ‘quasi-linear optimal perturbation’, i.e. the finite-amplitude manifestation of the underlying linear optimal perturbation. We also consider a wider flow geometry recently studied by Monokrousos et al. (Phys. Rev. Lett., vol. 106, 2011, 134502) and present evidence that the critical energy for transition
${E}_{0} \lt {E}_{c} $ , its maximum gain over all time intervals is always less than the equivalent maximum gain for the ‘quasi-linear optimal perturbation’, i.e. the finite-amplitude manifestation of the underlying linear optimal perturbation. We also consider a wider flow geometry recently studied by Monokrousos et al. (Phys. Rev. Lett., vol. 106, 2011, 134502) and present evidence that the critical energy for transition  ${E}_{c} $ they found by using total dissipation over a time interval as the optimizing functional is recovered using energy gain at a fixed target time as the optimizing functional, with the same associated minimal seed emerging. This emphasizes that the precise form of the functional does not appear to be important for identifying
${E}_{c} $ they found by using total dissipation over a time interval as the optimizing functional is recovered using energy gain at a fixed target time as the optimizing functional, with the same associated minimal seed emerging. This emphasizes that the precise form of the functional does not appear to be important for identifying 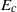 ${E}_{c} $ provided it takes heightened values for turbulent flows, as postulated by Pringle, Willis & Kerswell (J. Fluid Mech., vol. 703, 2012, pp. 415–443). All our results highlight the irrelevance of the linear energy gain optimal perturbation for predicting or describing the lowest-energy flow structure which triggers turbulence.
${E}_{c} $ provided it takes heightened values for turbulent flows, as postulated by Pringle, Willis & Kerswell (J. Fluid Mech., vol. 703, 2012, pp. 415–443). All our results highlight the irrelevance of the linear energy gain optimal perturbation for predicting or describing the lowest-energy flow structure which triggers turbulence.
Information
- Type
- Papers
- Information
- Copyright
- ©2012 Cambridge University Press
References
- 76
- Cited by

