Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Threadgill, James A. S.
Little, Jesse C.
and
Wernz, Stefan H.
2021.
Transitional Shock Boundary Layer Interactions on a Compression Ramp at Mach 4.
AIAA Journal,
Vol. 59,
Issue. 12,
p.
4824.
Paredes, Pedro
Scholten, Anton
Choudhari, Meelan M.
Li, Fei
Benitez, Elizabeth K.
and
Jewell, Joseph S.
2022.
Boundary-Layer Instabilities Over a Cone-Cylinder-Flare Model at Mach 6.
Li, Fei
Choudhari, Meelan M.
Paredes, Pedro
and
Scholten, Anton
2022.
Nonlinear Evolution of Instabilities in a Laminar Separation Bubble at Hypersonic Mach Number.
Lugrin, Mathieu
Beneddine, Samir
Garnier, Eric
and
Bur, Reynald
2022.
Multi-scale study of the transitional shock-wave boundary layer interaction in hypersonic flow.
Theoretical and Computational Fluid Dynamics,
Vol. 36,
Issue. 2,
p.
277.
Wang, Hongyu
Hu, Weibo
Xie, Feng
Li, Jie
Jia, Yao
and
Yang, Yanguang
2022.
Control effects of a high-frequency pulsed discharge on a hypersonic separated flow.
Physics of Fluids,
Vol. 34,
Issue. 6,
Cao, Shibin
Hao, Jiaao
Klioutchnikov, Igor
Wen, Chih-Yung
Olivier, Herbert
and
Heufer, Karl Alexander
2022.
Transition to turbulence in hypersonic flow over a compression ramp due to intrinsic instability.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Lugrin, Mathieu
Nicolas, François
Severac, Nicolas
Tobeli, Jean-Pierre
Beneddine, Samir
Garnier, Eric
Esquieu, Sebastien
and
Bur, Reynald
2022.
Transitional shockwave/boundary layer interaction experiments in the R2Ch blowdown wind tunnel.
Experiments in Fluids,
Vol. 63,
Issue. 2,
Franceschini, Lucas
Sipp, Denis
Marquet, Olivier
Moulin, Johann
and
Dandois, Julien
2022.
Identification and reconstruction of high-frequency fluctuations evolving on a low-frequency periodic limit cycle: application to turbulent cylinder flow.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Blanco, Diego C.P.
Martini, Eduardo
Sasaki, Kenzo
and
Cavalieri, André V.G.
2022.
Improved convergence of the spectral proper orthogonal decomposition through time shifting.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Zhu, W.K.
Gu, D.W.
Si, W.F.
Zhang, M.J.
Chen, S.Y.
Smith, C.R.
Zhu, Y.D.
and
Lee, C.B.
2022.
Instability evolution in the hypersonic boundary layer over a wavy wall.
Journal of Fluid Mechanics,
Vol. 943,
Issue. ,
Dwivedi, Anubhav
and
Jovanovic, Mihailo R.
2022.
A weakly nonlinear analysis of transition in a hypersonic flow.
p.
4171.
Dwivedi, Anubhav
Sidharth, G.S.
and
Jovanović, Mihailo R.
2022.
Oblique transition in hypersonic double-wedge flow.
Journal of Fluid Mechanics,
Vol. 948,
Issue. ,
Chen, Xi
Dong, Siwei
Tu, Guohua
Yuan, Xianxu
and
Chen, Jianqiang
2022.
Boundary layer transition and linear modal instabilities of hypersonic flow over a lifting body.
Journal of Fluid Mechanics,
Vol. 938,
Issue. ,
Fan, Jianhui
Hao, Jiaao
and
Wen, Chih-Yung
2022.
Nonlinear interactions of global instabilities in hypersonic laminar flow over a double cone.
Physics of Fluids,
Vol. 34,
Issue. 12,
Paredes, Pedro
Scholten, Anton
Choudhari, Meelan M.
Li, Fei
Benitez, Elizabeth K.
and
Jewell, Joseph S.
2022.
Boundary-Layer Instabilities over a Cone–Cylinder–Flare Model at Mach 6.
AIAA Journal,
Vol. 60,
Issue. 10,
p.
5652.
Ninni, Davide
Bonelli, Francesco
and
Pascazio, Giuseppe
2023.
Simulation of High-Enthalpy Turbulent Shock Wave/Boundary Layer Interaction Using a RANS Approach.
Aerotecnica Missili & Spazio,
Vol. 102,
Issue. 4,
p.
323.
Mahalingesh, Nikhil
Piponniau, Sébastien
and
Dupont, Pierre
2023.
Effects of Shock-Induced Separation on Boundary Layer Transitional Mechanisms.
Hao, Jiaao
Cao, Shibin
Guo, Peixu
and
Wen, Chih-Yung
2023.
Response of hypersonic compression corner flow to upstream disturbances.
Journal of Fluid Mechanics,
Vol. 964,
Issue. ,
Threadgill, James A.
Singh, Ashish
Roskelley Garcia, Alejandro
and
Little, Jesse C.
2023.
Boundary Layer Separation on a Hollow-Cylinder/Flare at Mach 5.
Kamal, Omar
Lakebrink, Matthew T.
and
Colonius, Tim
2023.
Global receptivity analysis: physically realizable input–output analysis.
Journal of Fluid Mechanics,
Vol. 956,
Issue. ,
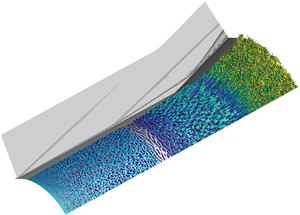
 $15^\circ$ axisymmetrical compression ramp is performed at a free stream Mach number of 5 and a transitional Reynolds number. The inlet of the computational domain is perturbed with a white noise in order to excite convective instabilities. Coherent structures are extracted using spectral proper orthogonal decomposition (SPOD), which gives a mathematically optimal decomposition of spatio-temporally correlated structures within the flow. The mean flow is used to perform a resolvent analysis in order to study non-normal linear amplification mechanisms. The comparison between the resolvent analysis and the SPOD results provides insight on both the linear and nonlinear mechanisms at play in the flow. To carry out the analysis, the flow is separated into three main regions of interest: the attached boundary layer, the mixing layer and the reattachment region. The observed transition process is dependent on the linear amplification of oblique modes in the boundary layer over a broad range of frequencies. These modes interact nonlinearly to create elongated streamwise structures which are then amplified by a linear mechanism in the rest of the domain until they break down in the reattachment region. The early nonlinear interaction is found to be essential for the transition process.
$15^\circ$ axisymmetrical compression ramp is performed at a free stream Mach number of 5 and a transitional Reynolds number. The inlet of the computational domain is perturbed with a white noise in order to excite convective instabilities. Coherent structures are extracted using spectral proper orthogonal decomposition (SPOD), which gives a mathematically optimal decomposition of spatio-temporally correlated structures within the flow. The mean flow is used to perform a resolvent analysis in order to study non-normal linear amplification mechanisms. The comparison between the resolvent analysis and the SPOD results provides insight on both the linear and nonlinear mechanisms at play in the flow. To carry out the analysis, the flow is separated into three main regions of interest: the attached boundary layer, the mixing layer and the reattachment region. The observed transition process is dependent on the linear amplification of oblique modes in the boundary layer over a broad range of frequencies. These modes interact nonlinearly to create elongated streamwise structures which are then amplified by a linear mechanism in the rest of the domain until they break down in the reattachment region. The early nonlinear interaction is found to be essential for the transition process.

