Article contents
Transition and turbulence in horizontal convection: linear stability analysis
Published online by Cambridge University Press: 16 May 2017
Abstract
The linear instability mechanisms of horizontal convection in a rectangular cavity forced by a horizontal buoyancy gradient along its surface are investigated using local and global stability analyses for a Prandtl number equal to unity. The results show that the stability of the base flow, a steady circulation characterized by a narrow descending plume and a broad upwelling region, depends on the Rayleigh number, 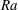 $Ra$ . For free-slip boundary conditions at a critical value of
$Ra$ . For free-slip boundary conditions at a critical value of 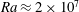 $Ra\approx 2\times 10^{7}$ , the steady base flow becomes unstable to three-dimensional perturbations, characterized by counter-rotating vortices originating within the plume region. A Wentzel–Kramers–Brillouin (WKB) method applied along closed streamlines demonstrates that this instability is of a Rayleigh–Taylor type and can be used to accurately reconstruct the global instability mode. In the case of no-slip boundary conditions, the base flow also becomes unstable to a self-sustained two-dimensional instability whose critical Rayleigh number is
$Ra\approx 2\times 10^{7}$ , the steady base flow becomes unstable to three-dimensional perturbations, characterized by counter-rotating vortices originating within the plume region. A Wentzel–Kramers–Brillouin (WKB) method applied along closed streamlines demonstrates that this instability is of a Rayleigh–Taylor type and can be used to accurately reconstruct the global instability mode. In the case of no-slip boundary conditions, the base flow also becomes unstable to a self-sustained two-dimensional instability whose critical Rayleigh number is 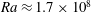 $Ra\approx 1.7\times 10^{8}$ . Beyond this critical
$Ra\approx 1.7\times 10^{8}$ . Beyond this critical 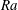 $Ra$ , two-dimensional equilibrium stationary states of the Navier–Stokes equations are computed using the selective frequency damping method. The two-dimensional onset of instability is shown to be characterized by a family of modes also originating within the plume. A local spatio-temporal stability analysis shows that the flow becomes absolutely unstable at the origin of the plume. Taken together, these results illustrate the mechanisms behind the onset of turbulence that has been observed in horizontal convection.
$Ra$ , two-dimensional equilibrium stationary states of the Navier–Stokes equations are computed using the selective frequency damping method. The two-dimensional onset of instability is shown to be characterized by a family of modes also originating within the plume. A local spatio-temporal stability analysis shows that the flow becomes absolutely unstable at the origin of the plume. Taken together, these results illustrate the mechanisms behind the onset of turbulence that has been observed in horizontal convection.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 17
- Cited by


