Article contents
Topology of interacting coiled vortex rings
Published online by Cambridge University Press: 03 September 2018
Abstract
Pairs of nested vortex rings, one with coils, are evolved numerically to compare their topological numbers to those of recent experiments reported in Scheeler et al. (Science, vol. 357, 2017, pp. 487–491). Included are the twist 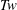 $Tw$, writhe
$Tw$, writhe 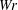 $Wr$ and self-linking
$Wr$ and self-linking 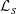 ${\mathcal{L}}_{S}$ numbers, plus centreline helicities
${\mathcal{L}}_{S}$ numbers, plus centreline helicities 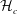 ${\mathcal{H}}_{c}$. The questions are: can the experimental numbers be validated and do these numbers have roles in the dynamics of the global helicities
${\mathcal{H}}_{c}$. The questions are: can the experimental numbers be validated and do these numbers have roles in the dynamics of the global helicities 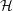 ${\mathcal{H}}$ and enstrophies
${\mathcal{H}}$ and enstrophies 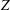 $Z$ with respect to cascades? Topological analysis of the experiments
$Z$ with respect to cascades? Topological analysis of the experiments 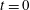 $t=0$ analytic centreline vortex trajectories validates only the writhe measurements, not their values of
$t=0$ analytic centreline vortex trajectories validates only the writhe measurements, not their values of 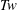 $Tw$ and
$Tw$ and 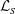 ${\mathcal{L}}_{S}$, which obey
${\mathcal{L}}_{S}$, which obey 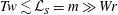 $Tw\lesssim {\mathcal{L}}_{S}=m\gg Wr$ for
$Tw\lesssim {\mathcal{L}}_{S}=m\gg Wr$ for 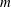 $m$-coil rings. Not
$m$-coil rings. Not 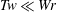 $Tw\ll Wr$. To suggest why the large twists do not contribute to
$Tw\ll Wr$. To suggest why the large twists do not contribute to 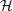 ${\mathcal{H}}$, it is noted that the mapping of the coiled rings onto the mesh is to a first approximation a single pair of Clebsch potentials, whose self-helicity
${\mathcal{H}}$, it is noted that the mapping of the coiled rings onto the mesh is to a first approximation a single pair of Clebsch potentials, whose self-helicity 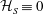 ${\mathcal{H}}_{S}\equiv 0$. Numerical rings with circulations
${\mathcal{H}}_{S}\equiv 0$. Numerical rings with circulations 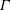 $\unicode[STIX]{x1D6E4}$, including some single rings, show small initial helicities with
$\unicode[STIX]{x1D6E4}$, including some single rings, show small initial helicities with 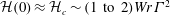 ${\mathcal{H}}(0)\approx {\mathcal{H}}_{c}\sim (\text{1 to 2})Wr\unicode[STIX]{x1D6E4}^{2}$
${\mathcal{H}}(0)\approx {\mathcal{H}}_{c}\sim (\text{1 to 2})Wr\unicode[STIX]{x1D6E4}^{2}$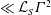 $\ll {\mathcal{L}}_{S}\unicode[STIX]{x1D6E4}^{2}$. For time and velocity scales that are consistent with the experiments, as the coils evolve, their
$\ll {\mathcal{L}}_{S}\unicode[STIX]{x1D6E4}^{2}$. For time and velocity scales that are consistent with the experiments, as the coils evolve, their 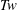 $Tw$,
$Tw$, 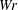 $Wr$,
$Wr$, 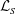 ${\mathcal{L}}_{S}$ numbers and their helicities are nearly static until reconnection. Nonetheless,
${\mathcal{L}}_{S}$ numbers and their helicities are nearly static until reconnection. Nonetheless, 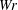 $Wr$ and
$Wr$ and 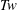 $Tw$ retain important complementary roles in the dynamics of the global helicity
$Tw$ retain important complementary roles in the dynamics of the global helicity 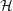 ${\mathcal{H}}$ and enstrophy
${\mathcal{H}}$ and enstrophy 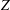 $Z$, with the evolution of the torsion
$Z$, with the evolution of the torsion 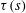 $\unicode[STIX]{x1D70F}(s)$ profile showing the beginnings of a cascade to small scales.
$\unicode[STIX]{x1D70F}(s)$ profile showing the beginnings of a cascade to small scales.
Information
- Type
- JFM Rapids
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 11
- Cited by


