Article contents
Three-dimensional structural characteristics of flow separation induced by a forward-facing step in a turbulent channel flow
Published online by Cambridge University Press: 26 May 2021
Abstract
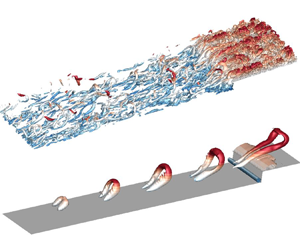
Separating and reattaching turbulent flows induced by a forward-facing step subjected to an incoming fully developed turbulent channel flow are studied using direct numerical simulation. The step height is one quarter of the channel height, and the Reynolds number based on friction velocity and half-channel height at the inlet is 180. The three-dimensional spatio-temporal characteristics of separation bubbles upstream and downstream of the step are analysed with particular attention to the effects of impinging hairpin structures and the topology of principal stretching. Immediately upstream of the step, the fluctuating vorticity parallel to the mean streamlines is significant. On the frontal surface of the step, strong spanwise skin friction appears in the form of alternating positive and negative values in vertical strips. Over the step, the principal stretching switches orientation along a curve emanating from the leading edge, which is termed the principal stretching line (PSL). The reverse flows upstream and downstream of the step possess dominant and harmonic frequencies that mirror those of the incoming flow. As a hairpin structure leans over the step, the associated vorticity is deformed by the principal stretching. Specifically, PSL marks the lower bound of the deformed hairpin legs, and an opposite-signed pair of counter-rotating quasi-streamwise vortices are induced near the top surface of the step. Consequently, the separation bubbles upstream of and over the step are enlarged and suppressed, respectively. For a sufficiently strong hairpin structure interacting with the step, an open-type separation occurs upstream of the step, while dual separation bubbles appear over the step.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 8
- Cited by


