Article contents
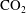 $\text{CO}_{2}$ dissolution in a background hydrological flow
$\text{CO}_{2}$ dissolution in a background hydrological flow
Published online by Cambridge University Press: 26 January 2016
Abstract
During 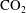 $\text{CO}_{2}$ sequestration into a deep saline aquifer of finite vertical extent,
$\text{CO}_{2}$ sequestration into a deep saline aquifer of finite vertical extent, 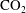 $\text{CO}_{2}$ will tend to accumulate in structural highs such as offered by an anticline. Over times of tens to thousands of years, some of the
$\text{CO}_{2}$ will tend to accumulate in structural highs such as offered by an anticline. Over times of tens to thousands of years, some of the 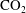 $\text{CO}_{2}$ will dissolve into the underlying groundwater to produce a region of relatively dense, saturated water directly below the plume of
$\text{CO}_{2}$ will dissolve into the underlying groundwater to produce a region of relatively dense, saturated water directly below the plume of 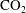 $\text{CO}_{2}$ . Continued dissolution then requires the supply of unsaturated aquifer water. In an aquifer of finite vertical extent, this may be provided by a background hydrological flow, or a laterally-spreading buoyancy-driven flow caused by the greater density of the
$\text{CO}_{2}$ . Continued dissolution then requires the supply of unsaturated aquifer water. In an aquifer of finite vertical extent, this may be provided by a background hydrological flow, or a laterally-spreading buoyancy-driven flow caused by the greater density of the 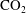 $\text{CO}_{2}$ saturated water relative to the original aquifer water.
$\text{CO}_{2}$ saturated water relative to the original aquifer water.
We investigate long time steady-state dissolution in the presence of a background hydrological flow. In steady state, the distribution of 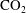 $\text{CO}_{2}$ in the groundwater upstream of the aquifer involves a balance between three competing effects: (i) the buoyancy-driven flow of
$\text{CO}_{2}$ in the groundwater upstream of the aquifer involves a balance between three competing effects: (i) the buoyancy-driven flow of 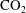 $\text{CO}_{2}$ saturated water; (ii) the diffusion of
$\text{CO}_{2}$ saturated water; (ii) the diffusion of 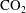 $\text{CO}_{2}$ from saturated to under-saturated water; and (iii) the advection associated with the oncoming background flow. This leads to three limiting regimes. In the limit of very slow diffusion, a nearly static intrusion of dense fluid may extend a finite distance upstream, balanced by the pressure gradient associated with the oncoming background flow. In the limit of fast diffusion relative to the flow, a gradient zone may become established in which the along-aquifer diffusive flux balances the advection associated with the background flow. However, if the buoyancy-driven flow speed exceeds the background hydrological flow speed, then a third, intermediate regime may become established. In this regime, a convective recirculation develops upstream of the anticline involving the vertical diffusion of
$\text{CO}_{2}$ from saturated to under-saturated water; and (iii) the advection associated with the oncoming background flow. This leads to three limiting regimes. In the limit of very slow diffusion, a nearly static intrusion of dense fluid may extend a finite distance upstream, balanced by the pressure gradient associated with the oncoming background flow. In the limit of fast diffusion relative to the flow, a gradient zone may become established in which the along-aquifer diffusive flux balances the advection associated with the background flow. However, if the buoyancy-driven flow speed exceeds the background hydrological flow speed, then a third, intermediate regime may become established. In this regime, a convective recirculation develops upstream of the anticline involving the vertical diffusion of 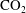 $\text{CO}_{2}$ from an upstream propagating flow of dense
$\text{CO}_{2}$ from an upstream propagating flow of dense 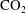 $\text{CO}_{2}$ saturated water into the downstream propagating flow of
$\text{CO}_{2}$ saturated water into the downstream propagating flow of 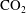 $\text{CO}_{2}$ unsaturated water. For each limiting case, we find analytical solutions for the distribution of
$\text{CO}_{2}$ unsaturated water. For each limiting case, we find analytical solutions for the distribution of 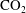 $\text{CO}_{2}$ upstream of the anticline, and test our analysis with full numerical simulations. A key result is that, although there may be very different controls on the distribution and extent of
$\text{CO}_{2}$ upstream of the anticline, and test our analysis with full numerical simulations. A key result is that, although there may be very different controls on the distribution and extent of 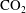 $\text{CO}_{2}$ bearing water upstream of the anticline, in each case the dissolution rate is given by the product of the background volume flux and the difference in concentration between the
$\text{CO}_{2}$ bearing water upstream of the anticline, in each case the dissolution rate is given by the product of the background volume flux and the difference in concentration between the 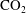 $\text{CO}_{2}$ saturated water and the original aquifer water upstream.
$\text{CO}_{2}$ saturated water and the original aquifer water upstream.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 16
- Cited by


