Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bhat, Farooq Ahmad
and
Samanta, Arghya
2019.
Linear stability analysis of a surfactant-laden shear-imposed falling film.
Physics of Fluids,
Vol. 31,
Issue. 5,
Rabbi, Khan Md.
Carter, Jake
and
Putnam, Shawn A.
2020.
Understanding pulsed jet impingement cooling by instantaneous heat flux matching at solid-liquid interfaces.
Physical Review Fluids,
Vol. 5,
Issue. 9,
Sani, Muhammad
Selvan, Siluvai Antony
Ghosh, Sukhendu
and
Behera, Harekrushna
2020.
Effect of imposed shear on the dynamics of a contaminated two-layer film flow down a slippery incline.
Physics of Fluids,
Vol. 32,
Issue. 10,
Trifonov, Yu.Ya.
2020.
Linear and nonlinear instabilities of a co-current gas-liquid flow between two inclined plates analyzed using the Navier–Stokes equations.
International Journal of Multiphase Flow,
Vol. 122,
Issue. ,
p.
103159.
Lavalle, Gianluca
Grenier, Nicolas
Mergui, Sophie
and
Dietze, Georg F.
2020.
Solitary waves on superconfined falling liquid films.
Physical Review Fluids,
Vol. 5,
Issue. 3,
Baingne, Mahendra
and
Sharma, Gaurav
2020.
Effect of wall deformability on the stability of shear-imposed film flow past an inclined plane.
International Journal of Engineering Science,
Vol. 150,
Issue. ,
p.
103243.
Kushnir, R.
Barmak, I.
Ullmann, A.
and
Brauner, N.
2021.
Stability of gravity-driven thin-film flow in the presence of an adjacent gas phase.
International Journal of Multiphase Flow,
Vol. 135,
Issue. ,
p.
103443.
Lavalle, Gianluca
Mergui, Sophie
Grenier, Nicolas
and
Dietze, Georg F.
2021.
Superconfined falling liquid films: linear versus nonlinear dynamics.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Mohamed, Omair A. A.
Dallaston, Michael C.
and
Biancofiore, Luca
2021.
Spatiotemporal evolution of evaporating liquid films sheared by a gas.
Physical Review Fluids,
Vol. 6,
Issue. 11,
Mendez, M.A.
Gosset, A.
Scheid, B.
Balabane, M.
and
Buchlin, J.-M.
2021.
Dynamics of the jet wiping process via integral models.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
Aktershev, S. P.
Alekseenko, S. V.
and
Tsvelodub, O. Yu.
2022.
Theoretical modeling of fluid dynamics and heat transfer in wavy liquid films under complex flow conditions (review).
Thermophysics and Aeromechanics,
Vol. 29,
Issue. 1,
p.
1.
Hossain, Md. Mouzakkir
and
Behera, Harekrushna
2022.
Shear-imposed falling thin Newtonian film over a porous slippery surface.
Physics of Fluids,
Vol. 34,
Issue. 11,
Jia, Beinan
and
Jian, Yongjun
2023.
Stability of a liquid film on inclined flexible substrates: Effect of the spontaneous odd viscosity.
Physical Review E,
Vol. 108,
Issue. 4,
Mohamed, Hammam
Sesterhenn, Jörn
and
Biancofiore, Luca
2023.
The effect of side walls on the stability of falling films.
Journal of Fluid Mechanics,
Vol. 964,
Issue. ,
Ishimura, Misa
Mergui, Sophie
Ruyer-Quil, Christian
and
Dietze, Georg F.
2023.
Gas-sheared falling liquid films beyond the absolute instability limit.
Journal of Fluid Mechanics,
Vol. 971,
Issue. ,
Hafez, N. M.
and
Assaf, Ahmed
2023.
Electrohydrodynamic stability and heat and mass transfer of a dielectric fluid flowing over an inclined plane through porous medium with external shear stress.
The European Physical Journal Plus,
Vol. 138,
Issue. 1,
Mergui, Sophie
Lavalle, Gianluca
Li, Yiqin
Grenier, Nicolas
and
Dietze, Georg F.
2023.
Nonlinear wave attenuation in strongly confined falling liquid films sheared by a laminar counter-current gas flow.
Journal of Fluid Mechanics,
Vol. 954,
Issue. ,
Botticini, P.
Lavalle, G.
Picchi, D.
and
Poesio, P.
2024.
Compressibility-induced destabilisation of falling liquid films: an integral approach.
International Journal of Multiphase Flow,
Vol. 171,
Issue. ,
p.
104667.
Zhao, Qishan
Li, Shicheng
and
Ma, Xuehu
2024.
Dual effects of pressure difference for long-wave stratified flow in horizontal microchannels.
Physics of Fluids,
Vol. 36,
Issue. 12,
Chattopadhyay, Souradip
Bijalwan, Ashutosh
and
Gaonkar, Amar K.
2024.
Shear-imposed falling film on a vertical moving plate with disrupted time-reversal.
Physica D: Nonlinear Phenomena,
Vol. 468,
Issue. ,
p.
134314.
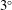 $3^{\circ }$ and of height 2.8 times the film thickness. We also identify the critical conditions for the full suppression of the instability in terms of the governing parameters. The stabilization is caused by the strong confinement of the gas, which produces perturbations of the adverse interfacial tangential shear stress that are shifted by half a wavelength with respect to the wavy film surface. This tends to reduce flow-rate variations within the film, thus attenuating the inertia-based driving mechanism of the Kapitza instability.
$3^{\circ }$ and of height 2.8 times the film thickness. We also identify the critical conditions for the full suppression of the instability in terms of the governing parameters. The stabilization is caused by the strong confinement of the gas, which produces perturbations of the adverse interfacial tangential shear stress that are shifted by half a wavelength with respect to the wavy film surface. This tends to reduce flow-rate variations within the film, thus attenuating the inertia-based driving mechanism of the Kapitza instability.