Article contents
Subgrid-scale structure and fluxes of turbulence underneath a surface wave
Published online by Cambridge University Press: 18 September 2019
Abstract
In this study, the behaviours of subgrid-scale (SGS) turbulence are investigated with direct numerical simulations when an isotropic turbulence is brought to interact with imposed rapid waves. A partition of the velocity field is used to decompose the SGS stress into three parts, namely, the turbulent part 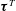 $\unicode[STIX]{x1D749}^{T}$, the wave-induced part
$\unicode[STIX]{x1D749}^{T}$, the wave-induced part 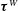 $\unicode[STIX]{x1D749}^{W}$ and the cross-interaction part
$\unicode[STIX]{x1D749}^{W}$ and the cross-interaction part 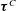 $\unicode[STIX]{x1D749}^{C}$. Under strong wave straining,
$\unicode[STIX]{x1D749}^{C}$. Under strong wave straining, 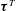 $\unicode[STIX]{x1D749}^{T}$ is found to follow the Kolmogorov scaling
$\unicode[STIX]{x1D749}^{T}$ is found to follow the Kolmogorov scaling 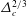 $\unicode[STIX]{x1D6E5}_{c}^{2/3}$, where
$\unicode[STIX]{x1D6E5}_{c}^{2/3}$, where 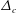 $\unicode[STIX]{x1D6E5}_{c}$ is the filter width. Based on the linear Airy wave theory,
$\unicode[STIX]{x1D6E5}_{c}$ is the filter width. Based on the linear Airy wave theory, 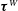 $\unicode[STIX]{x1D749}^{W}$ and the filtered strain-rate tensor due to the wave motion,
$\unicode[STIX]{x1D749}^{W}$ and the filtered strain-rate tensor due to the wave motion, 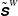 $\tilde{\unicode[STIX]{x1D64E}}^{W}$, are found to have different phases, posing a difficulty in applying the usual eddy-viscosity model. On the other hand,
$\tilde{\unicode[STIX]{x1D64E}}^{W}$, are found to have different phases, posing a difficulty in applying the usual eddy-viscosity model. On the other hand, 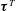 $\unicode[STIX]{x1D749}^{T}$ and the filtered strain-rate tensor due to the turbulent motion,
$\unicode[STIX]{x1D749}^{T}$ and the filtered strain-rate tensor due to the turbulent motion, 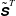 $\tilde{\unicode[STIX]{x1D64E}}^{T}$, are only weakly wave-phase-dependent and could be well related by an eddy-viscosity model. The linear wave theory is also used to describe the vertical distributions of SGS statistics driven by the wave-induced motion. The predictions are in good agreement with the direct numerical simulation results. The budget equation for the turbulent SGS kinetic energy shows that the transport terms related to turbulence are important near the free surface and they compensate the imbalance between the energy flux and the SGS energy dissipation.
$\tilde{\unicode[STIX]{x1D64E}}^{T}$, are only weakly wave-phase-dependent and could be well related by an eddy-viscosity model. The linear wave theory is also used to describe the vertical distributions of SGS statistics driven by the wave-induced motion. The predictions are in good agreement with the direct numerical simulation results. The budget equation for the turbulent SGS kinetic energy shows that the transport terms related to turbulence are important near the free surface and they compensate the imbalance between the energy flux and the SGS energy dissipation.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 1
- Cited by

