Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Musgrave, R. C.
MacKinnon, J. A.
Pinkel, R.
Waterhouse, A. F.
Nash, J.
and
Kelly, S. M.
2017.
The Influence of Subinertial Internal Tides on Near-Topographic Turbulence at the Mendocino Ridge: Observations and Modeling.
Journal of Physical Oceanography,
Vol. 47,
Issue. 8,
p.
2139.
Smith, Katharine A.
Merrifield, Mark A.
and
Carter, Glenn S.
2017.
Coastal‐trapped behavior of the diurnal internal tide at O'ahu, Hawai'i.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 5,
p.
4257.
Hughes, Kenneth G.
Klymak, Jody M.
Williams, William J.
and
Melling, Humfrey
2018.
Tidally Modulated Internal Hydraulic Flow and Energetics in the Central Canadian Arctic Archipelago.
Journal of Geophysical Research: Oceans,
Vol. 123,
Issue. 8,
p.
5210.
Kunze, Eric
and
Lien, Ren-Chieh
2019.
Energy Sinks for Lee Waves in Shear Flow.
Journal of Physical Oceanography,
Vol. 49,
Issue. 11,
p.
2851.
Hughes, Kenneth G.
and
Klymak, Jody M.
2019.
Tidal Conversion and Dissipation at Steep Topography in a Channel Poleward of the Critical Latitude.
Journal of Physical Oceanography,
Vol. 49,
Issue. 5,
p.
1269.
Parrish, Frank A.
and
Oliver, Thomas A.
2020.
Comparative Observations of Current Flow, Tidal Spectra, and Scattering Strength in and Around Hawaiian Deep-Sea Coral Patches.
Frontiers in Marine Science,
Vol. 7,
Issue. ,
Voisin, Bruno
2020.
Near-field internal wave beams in two dimensions.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Mazloff, Matthew R.
Cornuelle, Bruce
Gille, Sarah T.
and
Wang, Jinbo
2020.
The Importance of Remote Forcing for Regional Modeling of Internal Waves.
Journal of Geophysical Research: Oceans,
Vol. 125,
Issue. 2,
Fer, Ilker
Koenig, Zoé
Kozlov, Igor E.
Ostrowski, Marek
Rippeth, Tom P.
Padman, Laurie
Bosse, Anthony
and
Kolås, Eivind
2020.
Tidally Forced Lee Waves Drive Turbulent Mixing Along the Arctic Ocean Margins.
Geophysical Research Letters,
Vol. 47,
Issue. 16,
Voisin, Bruno
2021.
Boundary integrals for oscillating bodies in stratified fluids.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
van der Kaaden, Anna-Selma
Mohn, Christian
Gerkema, Theo
Maier, Sandra R.
de Froe, Evert
van de Koppel, Johan
Rietkerk, Max
Soetaert, Karline
and
van Oevelen, Dick
2021.
Feedbacks between hydrodynamics and cold-water coral mound development.
Deep Sea Research Part I: Oceanographic Research Papers,
Vol. 178,
Issue. ,
p.
103641.
Legg, Sonya
2021.
Mixing by Oceanic Lee Waves.
Annual Review of Fluid Mechanics,
Vol. 53,
Issue. 1,
p.
173.
Lenn, Yueng-Djern
Fer, Ilker
Timmermans, Mary-Louise
and
MacKinnon, Jennifer A.
2022.
Ocean Mixing.
p.
275.
Wang, Shuya
Cao, Anzhou
Li, Qun
and
Chen, Xu
2022.
Diurnal and semidiurnal internal waves on the southern slope of the Yermak Plateau.
Scientific Reports,
Vol. 12,
Issue. 1,
Baco, Amy R.
Parrish, Frank A.
Auscavitch, Steven
Cairns, Stephen
Mejia-Mercado, Beatriz E.
Biede, Virginia
Morgan, Nicole
Roark, E. Brendan
and
Brantley, W. Ben
2023.
Cold-Water Coral Reefs of the World.
Vol. 19,
Issue. ,
p.
261.
Klema, Matthew R.
and
Venayagamoorthy, Subhas K.
2024.
Energetics of mode-1 internal waves interacting with topographic ridges of varying height and slope.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
Tan, Jiao
Chen, Xu
and
Meng, Jing
2025.
Impact of Earth's Rotation on the Nonlinear Evolution of Internal Tide Beams: Insights From Laboratory Experiments.
Journal of Geophysical Research: Oceans,
Vol. 130,
Issue. 8,
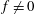 $f\neq 0$ , nonlinear processes lead to the formation of along-ridge jets, which become faster at high latitudes. Dissipation and mixing is larger, and peaks later in the tidal cycle when the tide is subinertial compared with when the tide is superinertial. Mixing occurs mainly on the flanks of the topography in both cases, though a superinertial tide may additionally generate mixing above topography arising from convective breaking of radiating waves.
$f\neq 0$ , nonlinear processes lead to the formation of along-ridge jets, which become faster at high latitudes. Dissipation and mixing is larger, and peaks later in the tidal cycle when the tide is subinertial compared with when the tide is superinertial. Mixing occurs mainly on the flanks of the topography in both cases, though a superinertial tide may additionally generate mixing above topography arising from convective breaking of radiating waves.

