Article contents
Steady and transient response of a laminar separation bubble to controlled disturbances
Published online by Cambridge University Press: 26 January 2017
Abstract
The steady and transient response of a laminar separation bubble to flow disturbances is examined experimentally. Wind tunnel experiments are performed on a NACA 0012 aerofoil at a chord Reynolds number of 130 000 and angle of attack of 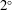 $2^{\circ }$ . Under the investigated conditions, a laminar separation bubble forms on the suction side of the aerofoil in the unperturbed flow. Periodic disturbances are introduced into the boundary layer just upstream of separation by means of a surface-mounted dielectric barrier discharge plasma actuator. Two-component, time-resolved particle image velocimetry measurements are performed to characterise both quasi-steady and transient response of the flow to periodic disturbances. The results show that the dynamics of the laminar separation bubble is dominated by the periodic shedding of shear layer vortices, forming upstream of the mean reattachment location due to the amplification of unstable flow disturbances. Introducing the controlled perturbations leads to significant changes in separation bubble topology and the characteristics of the dominant coherent structures, with the effect dependent on both amplitude and frequency of disturbances. Linear stability analysis demonstrates that the induced changes to the mean bubble topology affect the stability characteristics, reducing the maximum growth rate and the frequency of the most amplified disturbances by 35 % and 20 %, respectively, when the bubble length is reduced by up to 40 %. The observed changes in stability characteristics are shown to correlate with the attendant variations in the shape factor. The transient response of the bubble is associated with significant changes in the separation bubble dynamics, with significant differences observed between the relative duration (
$2^{\circ }$ . Under the investigated conditions, a laminar separation bubble forms on the suction side of the aerofoil in the unperturbed flow. Periodic disturbances are introduced into the boundary layer just upstream of separation by means of a surface-mounted dielectric barrier discharge plasma actuator. Two-component, time-resolved particle image velocimetry measurements are performed to characterise both quasi-steady and transient response of the flow to periodic disturbances. The results show that the dynamics of the laminar separation bubble is dominated by the periodic shedding of shear layer vortices, forming upstream of the mean reattachment location due to the amplification of unstable flow disturbances. Introducing the controlled perturbations leads to significant changes in separation bubble topology and the characteristics of the dominant coherent structures, with the effect dependent on both amplitude and frequency of disturbances. Linear stability analysis demonstrates that the induced changes to the mean bubble topology affect the stability characteristics, reducing the maximum growth rate and the frequency of the most amplified disturbances by 35 % and 20 %, respectively, when the bubble length is reduced by up to 40 %. The observed changes in stability characteristics are shown to correlate with the attendant variations in the shape factor. The transient response of the bubble is associated with significant changes in the separation bubble dynamics, with significant differences observed between the relative duration (  ${\approx}45\,\%$ ) of the transients flow response associated with the introduction and removal of the controlled disturbances. A detailed analysis of the results offers new insight into the response of laminar separation bubbles to changes in the disturbance environment.
${\approx}45\,\%$ ) of the transients flow response associated with the introduction and removal of the controlled disturbances. A detailed analysis of the results offers new insight into the response of laminar separation bubbles to changes in the disturbance environment.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 82
- Cited by


