Article contents
Stability transitions and turbulence in horizontal convection
Published online by Cambridge University Press: 25 June 2014
Abstract
Recent results have shown that convection forced by a temperature gradient along one horizontal boundary of a rectangular domain at a large Rayleigh number can be turbulent in parts of the flow field. However, the conditions for onset of turbulence, the dependence of flow and heat transport on Rayleigh number, and the roles of large and small scales in the flow, have not been established. We use three-dimensional direct numerical simulation (DNS) and large-eddy simulation (LES) over a wide range of Rayleigh numbers, 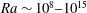 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Ra\sim 10^8\mbox{--}10^{15}$ , for Prandtl number
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Ra\sim 10^8\mbox{--}10^{15}$ , for Prandtl number 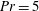 $Pr=5$ and a small aspect ratio, and show that a sequence of several stability transitions at
$Pr=5$ and a small aspect ratio, and show that a sequence of several stability transitions at 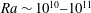 $Ra \sim 10^{10}\mbox{--} 10^{11}$ defines a change from laminar to turbulent flow. The Prandtl number dependence too is examined at
$Ra \sim 10^{10}\mbox{--} 10^{11}$ defines a change from laminar to turbulent flow. The Prandtl number dependence too is examined at 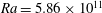 $Ra = 5.86 \times 10^{11}$ . At the smallest
$Ra = 5.86 \times 10^{11}$ . At the smallest 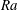 $Ra$ considered the thermal boundary layer is characterized by a balance of viscous stress and buoyancy, whereas inertia and buoyancy dominate in the large-
$Ra$ considered the thermal boundary layer is characterized by a balance of viscous stress and buoyancy, whereas inertia and buoyancy dominate in the large- 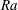 $Ra$ regime. The change in the momentum balance is accompanied by turbulent enhancement of the overall heat transfer, although both laminar and turbulent regimes give
$Ra$ regime. The change in the momentum balance is accompanied by turbulent enhancement of the overall heat transfer, although both laminar and turbulent regimes give 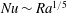 $Nu\sim Ra^{1/5}$ . The results support both viscous and inviscid theoretical scaling models from previous work. The mechanical energy budget for an intermediate range of Rayleigh numbers above onset of instability (
$Nu\sim Ra^{1/5}$ . The results support both viscous and inviscid theoretical scaling models from previous work. The mechanical energy budget for an intermediate range of Rayleigh numbers above onset of instability ( 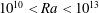 $10^{10}<Ra<10^{13}$ ) reveals that the small scales of motion are produced predominantly by thermal convection, whereas at
$10^{10}<Ra<10^{13}$ ) reveals that the small scales of motion are produced predominantly by thermal convection, whereas at 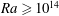 $Ra \ge 10^{14}$ shear instability of the large-scale flow begins to play a dominant role in sustaining the small-scale turbulence. Extrapolation to ocean conditions requires knowledge of the inertial regime identified here, but the simulations show that the corresponding asymptotic balance has not been fully realized by
$Ra \ge 10^{14}$ shear instability of the large-scale flow begins to play a dominant role in sustaining the small-scale turbulence. Extrapolation to ocean conditions requires knowledge of the inertial regime identified here, but the simulations show that the corresponding asymptotic balance has not been fully realized by 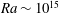 $Ra \sim 10^{15}$ .
$Ra \sim 10^{15}$ .
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 56
- Cited by

