Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mashayek, A.
Caulfield, C. P.
and
Peltier, W. R.
2013.
Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux.
Journal of Fluid Mechanics,
Vol. 736,
Issue. ,
p.
570.
Watanabe, Takashi
Toya, Yorinobu
and
Hara, Shota
2014.
Development and Flow Modes of Vertical Taylor-Couette System with Free Surface.
World Journal of Mechanics,
Vol. 04,
Issue. 03,
p.
90.
Deusebio, Enrico
Caulfield, C. P.
and
Taylor, J. R.
2015.
The intermittency boundary in stratified plane Couette flow.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
298.
Olsthoorn, Jason
and
Dalziel, Stuart B.
2015.
Vortex-ring-induced stratified mixing.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
113.
Manucharyan, G. E.
and
Caulfield, C. P.
2015.
Entrainment and mixed layer dynamics of a surface-stress-driven stratified fluid.
Journal of Fluid Mechanics,
Vol. 765,
Issue. ,
p.
653.
Maffioli, A.
Brethouwer, G.
and
Lindborg, E.
2016.
Mixing efficiency in stratified turbulence.
Journal of Fluid Mechanics,
Vol. 794,
Issue. ,
Lucas, Dan
Caulfield, C. P.
and
Kerswell, Rich R.
2017.
Layer formation in horizontally forced stratified turbulence: connecting exact coherent structures to linear instabilities.
Journal of Fluid Mechanics,
Vol. 832,
Issue. ,
p.
409.
Zhou, Qi
Taylor, J. R.
Caulfield, C. P.
and
Linden, P. F.
2017.
Diapycnal mixing in layered stratified plane Couette flow quantified in a tracer-based coordinate.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
p.
198.
Zhou, Qi
Taylor, John R.
and
Caulfield, C. P.
2017.
Self-similar mixing in stratified plane Couette flow for varying Prandtl number.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
86.
Eaves, T. S.
and
Caulfield, C. P.
2017.
Multiple instability of layered stratified plane Couette flow.
Journal of Fluid Mechanics,
Vol. 813,
Issue. ,
p.
250.
Facchini, Giulio
Favier, Benjamin
Le Gal, Patrice
Wang, Meng
and
Le Bars, Michael
2018.
The linear instability of the stratified plane Couette flow.
Journal of Fluid Mechanics,
Vol. 853,
Issue. ,
p.
205.
Ponetti, G.
Balmforth, N. J.
and
Eaves, T. S.
2018.
Instabilities in a staircase stratified shear flow.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 112,
Issue. 1,
p.
1.
Lucas, Dan
Caulfield, C. P.
and
Kerswell, Rich R.
2019.
Layer formation and relaminarisation in plane Couette flow with spanwise stratification.
Journal of Fluid Mechanics,
Vol. 868,
Issue. ,
p.
97.
Petrolo, Diana
and
Woods, Andrew W.
2019.
Measurements of buoyancy flux in a stratified turbulent flow.
Journal of Fluid Mechanics,
Vol. 861,
Issue. ,
Garaud, P.
2020.
Horizontal Shear Instabilities at Low Prandtl Number.
The Astrophysical Journal,
Vol. 901,
Issue. 2,
p.
146.
Petrolo, Diana
and
Longo, Sandro
2020.
Buoyancy transfer in a two-layer system in steady state. Experiments in a Taylor–Couette cell.
Journal of Fluid Mechanics,
Vol. 896,
Issue. ,
Langham, Jake
Eaves, Tom S.
and
Kerswell, Rich R.
2020.
Stably stratified exact coherent structures in shear flow: the effect of Prandtl number.
Journal of Fluid Mechanics,
Vol. 882,
Issue. ,
Chong, Kai Leong
Yang, Rui
Wang, Qi
Verzicco, Roberto
and
Lohse, Detlef
2020.
Café latte: spontaneous layer formation in laterally cooled double diffusive convection.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Caulfield, Colm-cille P.
2020.
Open questions in turbulent stratified mixing: Do we even know what we do not know?.
Physical Review Fluids,
Vol. 5,
Issue. 11,
Cope, Laura
Garaud, P.
and
Caulfield, C. P.
2020.
The dynamics of stratified horizontal shear flows at low Péclet number.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
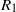 ${R}_{1} $ , and rotation rate,
${R}_{1} $ , and rotation rate, 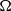 $\Omega $ , relative to the fixed outer cylinder, of radius
$\Omega $ , relative to the fixed outer cylinder, of radius 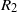 ${R}_{2} $ , as well as the initial buoyancy frequency
${R}_{2} $ , as well as the initial buoyancy frequency 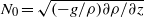 ${N}_{0} = \sqrt{(- g/ \rho )\partial \rho / \partial z} $ . We find that a linear stratification spontaneously splits into a series of layers and interfaces. The characteristic height of these layers is proportional to
${N}_{0} = \sqrt{(- g/ \rho )\partial \rho / \partial z} $ . We find that a linear stratification spontaneously splits into a series of layers and interfaces. The characteristic height of these layers is proportional to 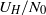 ${U}_{H} / {N}_{0} $ , where
${U}_{H} / {N}_{0} $ , where 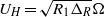 ${U}_{H} = \sqrt{{R}_{1} { \mathrm{\Delta} }_{R} } \Omega $ is a horizontal velocity scale, with
${U}_{H} = \sqrt{{R}_{1} { \mathrm{\Delta} }_{R} } \Omega $ is a horizontal velocity scale, with 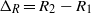 ${ \mathrm{\Delta} }_{R} = {R}_{2} - {R}_{1} $ the gap width of the annulus. The buoyancy flux through these layers matches the equivalent flux through a two-layer stratification, independently of the height or number of layers. For a strongly stratified flow, the flux tends to an asymptotic constant value, even when multiple layers are present, consistent with Woods et al. (J. Fluid Mech., vol. 663, 2010, pp. 347–357). For smaller stratification the flux increases, reaching a maximum just before the layers disappear due to overturning of the interfaces.
${ \mathrm{\Delta} }_{R} = {R}_{2} - {R}_{1} $ the gap width of the annulus. The buoyancy flux through these layers matches the equivalent flux through a two-layer stratification, independently of the height or number of layers. For a strongly stratified flow, the flux tends to an asymptotic constant value, even when multiple layers are present, consistent with Woods et al. (J. Fluid Mech., vol. 663, 2010, pp. 347–357). For smaller stratification the flux increases, reaching a maximum just before the layers disappear due to overturning of the interfaces.
