Article contents
Small-solid-fraction approximations for the slip-length tensor of micropillared superhydrophobic surfaces
Published online by Cambridge University Press: 26 March 2018
Abstract
Fakir-like superhydrophobic surfaces, formed by doubly periodic arrays of thin pillars that sustain a lubricating gas layer, exhibit giant liquid-slip lengths that scale as 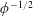 $\unicode[STIX]{x1D719}^{-1/2}$ relative to the periodicity,
$\unicode[STIX]{x1D719}^{-1/2}$ relative to the periodicity, 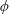 $\unicode[STIX]{x1D719}$ being the solid fraction (Ybert et al., Phys. Fluids, vol. 19, 2007, 123601). Considering arbitrarily shaped pillars distributed over an arbitrary Bravais lattice, we employ matched asymptotic expansions to calculate the slip-length tensor in the limit
$\unicode[STIX]{x1D719}$ being the solid fraction (Ybert et al., Phys. Fluids, vol. 19, 2007, 123601). Considering arbitrarily shaped pillars distributed over an arbitrary Bravais lattice, we employ matched asymptotic expansions to calculate the slip-length tensor in the limit 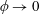 $\unicode[STIX]{x1D719}\rightarrow 0$. The leading
$\unicode[STIX]{x1D719}\rightarrow 0$. The leading 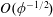 $O(\unicode[STIX]{x1D719}^{-1/2})$ slip length is determined from a local analysis of an ‘inner’ region close to a single pillar, in conjunction with a global force balance. This leading term, which is independent of the lattice geometry, is related to the drag due to pure translation of a flattened disk shaped like the pillar cross-section; its calculation is illustrated for the case of elliptical pillars. The
$O(\unicode[STIX]{x1D719}^{-1/2})$ slip length is determined from a local analysis of an ‘inner’ region close to a single pillar, in conjunction with a global force balance. This leading term, which is independent of the lattice geometry, is related to the drag due to pure translation of a flattened disk shaped like the pillar cross-section; its calculation is illustrated for the case of elliptical pillars. The 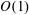 $O(1)$ slip length is associated with the excess velocity induced about a given pillar by all the others. Since the field induced by each pillar corresponds on the ‘outer’ lattice scale to a Stokeslet whose strength is fixed by the shear rate, the
$O(1)$ slip length is associated with the excess velocity induced about a given pillar by all the others. Since the field induced by each pillar corresponds on the ‘outer’ lattice scale to a Stokeslet whose strength is fixed by the shear rate, the 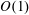 $O(1)$ slip length depends upon the lattice geometry but is independent of the cross-sectional shape. Its calculation entails asymptotic evaluation of singular lattice sums. Our approximations are in excellent agreement with existing numerical computations for both circular and square pillars.
$O(1)$ slip length depends upon the lattice geometry but is independent of the cross-sectional shape. Its calculation entails asymptotic evaluation of singular lattice sums. Our approximations are in excellent agreement with existing numerical computations for both circular and square pillars.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 9
- Cited by

