Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-25T09:37:25.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Shear thickening of a non-colloidal suspension with a viscoelastic matrix

Published online by Cambridge University Press:  18 October 2019

Adolfo Vázquez-Quesada Open the ORCID record for Adolfo Vázquez-Quesada [Opens in a new window] ,
Pep Español ,
Roger I. Tanner  and
Marco Ellero
Adolfo Vázquez-Quesada*
Affiliation:
Department of Theoretical Condensed Matter Physics, Universidad Autónoma de Madrid, 28049 Madrid, Spain
Pep Español*
Affiliation:
Departamento de Física Fundamental, UNED, Apartado 60141, 28080 Madrid, Spain
Roger I. Tanner*
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, University of Sydney, Sydney, NSW 2006, Australia
Marco Ellero*
Affiliation:
Basque Center for Applied Mathematics (BCAM), Alameda de Mazarredo 14, 48400 Bilbao, Spain IKERBASQUE, Basque Foundation for Science, Calle de María Díaz de Haro 3, 48013 Bilbao, Spain Zienkiewicz Centre for Computational Engineering (ZCCE), Swansea University, Bay Campus, Swansea SA1 8QQ, UK
*
†Email addresses for correspondence: adolfo.vazquez@uam.es, pep@fisfun.uned.es, roger.tanner@sydney.edu.au, mellero@bcamath.org
†Email addresses for correspondence: adolfo.vazquez@uam.es, pep@fisfun.uned.es, roger.tanner@sydney.edu.au, mellero@bcamath.org
†Email addresses for correspondence: adolfo.vazquez@uam.es, pep@fisfun.uned.es, roger.tanner@sydney.edu.au, mellero@bcamath.org
†Email addresses for correspondence: adolfo.vazquez@uam.es, pep@fisfun.uned.es, roger.tanner@sydney.edu.au, mellero@bcamath.org
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the rheology of a non-colloidal suspension of rigid spherical particles interacting with a viscoelastic matrix. Three-dimensional numerical simulations under shear flow are performed using the smoothed particle hydrodynamics method and compared with experimental data available in the literature using different constant-viscosity elastic Boger fluids. The rheological properties of the Boger matrices are matched in simulation under viscometric flow conditions. Suspension rheology under dilute to semi-concentrated conditions (i.e. up to solid volume fraction 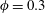$\unicode[STIX]{x1D719}=0.3$) is explored. It is found that at small Deborah numbers 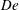$De$ (based on the macroscopic imposed shear rate), relative suspension viscosities 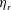$\unicode[STIX]{x1D702}_{r}$ exhibit a plateau at every concentration investigated. By increasing 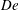$De$, shear thickening is observed, which is related to the extensional thickening of the underlying viscoelastic matrix. Under dilute conditions (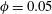$\unicode[STIX]{x1D719}=0.05$), numerical results for 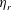$\unicode[STIX]{x1D702}_{r}$ agree quantitatively with experimental data in both the 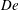$De$ and 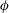$\unicode[STIX]{x1D719}$ dependences. Even under dilute conditions, simulations of full many-particle systems with no a priori specification of their spatial distribution need to be considered to recover precisely experimental values. By increasing the solid volume fraction towards 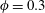$\unicode[STIX]{x1D719}=0.3$, despite the fact that the trend is well captured, the agreement remains qualitative with discrepancies arising in the absolute values of 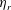$\unicode[STIX]{x1D702}_{r}$ obtained from simulations and experiments but also with large deviations existing among different experiments. With regard to the specific mechanism of elastic thickening, the microstructural analysis shows that elastic thickening correlates well with the average viscoelastic dissipation function 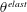$\unicode[STIX]{x1D703}^{elast}$, requiring a scaling as 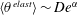$\langle \unicode[STIX]{x1D703}^{elast}\rangle \sim De^{\unicode[STIX]{x1D6FC}}$ with 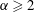$\unicode[STIX]{x1D6FC}\geqslant 2$ to take place. Locally, despite the fact that regions of large polymer stretching (and viscoelastic dissipation) can occur everywhere in the domain, flow regions uniquely responsible for the elastic thickening are well correlated to areas with significant extensional component.

JFM classification

Complex Fluids: Suspensions Non-Newtonian Flows: Viscoelasticity Non-Newtonian Flows: Rheology
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 1070 - 1094
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Batchelor, G. K. & Green, J. T. 1972 The determination of the bulk stress in a suspension of spherical particles to order c 2 . J. Fluid Mech. 56 (3), 401–427.10.1017/S0022112072002435Google Scholar
Bertevas, E., Fan, X. & Tanner, R. I. 2010 Simulation of the rheological properties of suspensions of oblate spheroidal particles in a Newtonian fluid. Rheol. Acta 49 (1), 53–73.10.1007/s00397-009-0390-8Google Scholar
Bian, X. & Ellero, M. 2014 A splitting integration scheme for the SPH simulation of concentrated particle suspensions. Comput. Phys. Commun. 185 (1), 53–62.10.1016/j.cpc.2013.08.015Google Scholar
Bian, X., Litvinov, S., Qian, R., Marco, E. & Nikolaus, A. 2012 Multiscale modeling of particle in suspension with smoothed dissipative particle dynamics. Phys. Fluids 24 (1), 012002.10.1063/1.3676244Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20 (1), 111–157.10.1146/annurev.fl.20.010188.000551Google Scholar
Cheal, O. & Ness, C. 2018 Rheology of dense granular suspensions under extensional flow. J. Rheol. 62 (2), 501–512.10.1122/1.5004007Google Scholar
Dai, S.-C., Qi, F. & Tanner, R. I. 2014 Viscometric functions of concentrated non-colloidal suspensions of spheres in a viscoelastic matrix. J. Rheol. 58 (1), 183–198.10.1122/1.4851336Google Scholar
D’Avino, G., Greco, F., Hulsen, M. A. & Maffettone, P. L. 2013 Rheology of viscoelastic suspensions of spheres under small and large amplitude oscillatory shear by numerical simulations. J. Rheol. 57 (3), 813–839.10.1122/1.4798626Google Scholar
D’Avino, G., Hulsen, M. A., Snijkers, F., Vermant, J., Greco, F. & Maffettone, P. L. 2008 Rotation of a sphere in a viscoelastic liquid subjected to shear flow. Part I: Simulation results. J. Rheol. 52 (6), 1331–1346.10.1122/1.2998219Google Scholar
Denn, M. M., Morris, J. F. & Bonn, D. 2018 Shear thickening in concentrated suspensions of smooth spheres in Newtonian suspending fluids. Soft Matt. 14, 170–184.Google Scholar
Einstein, A. 1906 Eine neue Bestimmung der Molekuldimensionen (in German). Annalen der Physik 324 (2), 289–306.10.1002/andp.19063240204Google Scholar
Einstein, A. 1911 Berichtigung zu meiner Arbeit: Eine neue Bestimmung der Molekuldimensionen (in German). Annalen der Physik 339 (3), 591–592.10.1002/andp.19113390313Google Scholar
Ellero, M. & Adams, N. A. 2011 SPH simulations of flow around a periodic array of cylinders confined in a channel. Intl J. Numer. Meth. Engng 86 (8), 1027–1040.10.1002/nme.3088Google Scholar
Ellero, M., Serrano, M. & Español, P. 2007 Incompressible smoothed particle hydrodynamics. J. Comput. Phys. 226 (2), 1731–1752.10.1016/j.jcp.2007.06.019Google Scholar
Fattal, R. & Kupferman, R. 2004 Constitutive laws for the matrix-logarithm of the conformation tensor. J. Non-Newtonian Fluid Mech. 123 (2), 281–285.10.1016/j.jnnfm.2004.08.008Google Scholar
Gallier, S., Lemaire, E., Peters, François & Laurent, L. 2014 Rheology of sheared suspensions of rough frictional particles. J. Fluid Mech. 757, 514–549.10.1017/jfm.2014.507Google Scholar
Grmela, M. & Öttinger, H. C. 1997 Dynamics and thermodynamics of complex fluids. I. development of a general formalism. Phys. Rev. E 56, 6620–6632.Google Scholar
Hemingway, E. J., Clarke, A., Pearson, J. R. A. & Fielding, S. M. 2018 Thickening of viscoelastic flow in a model porous medium. J. Non-Newtonian Fluid Mech. 251, 56–68.10.1016/j.jnnfm.2017.11.002Google Scholar
Housiadas, K. D. & Tanner, R. I. 2011 The angular velocity of a freely rotating sphere in a weakly viscoelastic matrix fluid. Phys. Fluids 23 (5), 051702.10.1063/1.3583376Google Scholar
Hwang, W. R., Hulsen, M. A., Meijer, H. E. H. & Kwon, T. H. 2004a Direct numerical simulations of suspensions of spherical particles in a viscoelastic fluid in sliding tri-periodic domains. In Proceedings of the XIVth International Congress on Rheology, August 22-27, 2004, Seoul, Republic of Korea (ed. Lee, J. W. & Lee, S. J.), pp. CR10–1 to CR10–3.Google Scholar
Hwang, W. R., Hulsen, M. A. & Meijer, H. E. H. 2004b Direct simulations of particle suspensions in a viscoelastic fluid in sliding bi-periodic frames. J. Non-Newtonian Fluid Mech. 121 (1), 15–33.Google Scholar
Mari, R., Seto, R., Morris, J. F. & Denn, M. M. 2014 Shear thickening, frictionless and frictional rheologies in non-Brownian suspensions. J. Rheol. 58 (6), 1693–1724.10.1122/1.4890747Google Scholar
Monaghan, J. J. 2005 Smoothed particle hydrodynamics. Rep. Prog. Phys. 68 (8), 1703–1759.10.1088/0034-4885/68/8/R01Google Scholar
Morris, J. P., Fox, P. J. & Zhu, Y. 1997 Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 136 (1), 214–226.10.1006/jcph.1997.5776Google Scholar
Ottinger, H. C. 2005 Complex Fluids. pp. 97–156. John Wiley & Sons.Google Scholar
Owens, R. G. & Phillips, T. N. 2002 Computational Rheology. Imperial College Press.10.1142/p160Google Scholar
Pasquino, R., Grizzuti, N., Maffettone, P. L. & Greco, F. 2008 Rheology of dilute and semidilute noncolloidal hard sphere suspensions. J. Rheol. 52 (6), 1369–1384.Google Scholar
Sbalzarini, I. F., Walther, J. H., Bergdorf, M., Hieber, S. E., Kotsalis, E. M. & Koumoutsakos, P. 2006 PPM – a highly efficient parallel particle–mesh library for the simulation of continuum systems. J. Comput. Phys. 215 (2), 566–588.10.1016/j.jcp.2005.11.017Google Scholar
Scirocco, R., Vermant, J. & Mewis, J. 2005 Shear thickening in filled boger fluids. J. Rheol. 49 (2), 551–567.10.1122/1.1849185Google Scholar
Sierou, A. & Brady, J. F. 2002 Rheology and microstructure in concentrated noncolloidal suspensions. J. Rheol. 46 (5), 1031–1056.10.1122/1.1501925Google Scholar
Snijkers, F., D’Avino, G., Maffettone, P. L., Greco, F., Hulsen, M. & Vermant, J. 2009 Rotation of a sphere in a viscoelastic liquid subjected to shear flow. Part II. experimental results. J. Rheol. 53 (2), 459–480.10.1122/1.3073052Google Scholar
Snijkers, F., D’Avino, G., Maffettone, P. L., Greco, F., Hulsen, M. A. & Vermant, J. 2011 Effect of viscoelasticity on the rotation of a sphere in shear flow. J. Non-Newtonian Fluid Mech. 166 (7), 363–372.Google Scholar
Vaithianathan, T. & Collins, L. R. 2003 Numerical approach to simulating turbulent flow of a viscoelastic polymer solution. J. Comput. Phys. 187 (1), 1–21.10.1016/S0021-9991(03)00028-7Google Scholar
Vázquez-Quesada, A., Bian, X. & Ellero, M. 2016a Three-dimensional simulations of dilute and concentrated suspensions using smoothed particle hydrodynamics. Comput. Part. Mech. 3 (2), 167–178.10.1007/s40571-015-0072-5Google Scholar
Vázquez-Quesada, A. & Ellero, M. 2016 Rheology and microstructure of non-colloidal suspensions under shear studied with smoothed particle hydrodynamics. J. Non-Newtonian Fluid Mech. 233, 37–47.Google Scholar
Vázquez-Quesada, A. & Ellero, M. 2017 SPH modeling and simulation of spherical particles interacting in a viscoelastic matrix. Phys. Fluids 29 (12), 121609.10.1063/1.4993610Google Scholar
Vázquez-Quesada, A., Ellero, M. & Español, P. 2009 Smoothed particle hydrodynamic model for viscoelastic fluids with thermal fluctuations. Phys. Rev. E 79 (5), 056707.Google Scholar
Vázquez-Quesada, A., Ellero, M. & Español, P. 2012 A SPH-based particle model for computational microrheology. Microfluid Nanofluid 13 (2), 249–260.10.1007/s10404-012-0954-2Google Scholar
Vázquez-Quesada, A., Mahmud, A., Dai, S., Ellero, M. & Tanner, R. I. 2017 Investigating the causes of shear-thinning in non-colloidal suspensions: Experiments and simulations. J. Non-Newtonian Fluid Mech. 248, 1–7.10.1016/j.jnnfm.2017.08.005Google Scholar
Vázquez-Quesada, A., Tanner, R. I. & Ellero, M. 2016b Shear thinning of noncolloidal suspensions. Phys. Rev. Lett. 117, 108001.10.1103/PhysRevLett.117.108001Google Scholar
Wapperom, P. & Hulsen, M. A. 1998 Thermodynamics of viscoelastic fluids: The temperature equation. J. Rheol. 42 (5), 999–1019.10.1122/1.550922Google Scholar
Yang, M., Krishnan, S. & Shaqfeh, E. S. G. 2016 Numerical simulations of the rheology of suspensions of rigid spheres at low volume fraction in a viscoelastic fluid under shear. J. Non-Newtonian Fluid Mech. 234, 51–68.10.1016/j.jnnfm.2016.04.003Google Scholar
Yang, M. & Shaqfeh, E. S. G. 2018a Mechanism of shear thickening in suspensions of rigid spheres in boger fluids. Part I: Dilute suspensions. J. Rheol. 62 (6), 1363–1377.10.1122/1.5024696Google Scholar
Yang, M. & Shaqfeh, E. S. G. 2018b Mechanism of shear thickening in suspensions of rigid spheres in boger fluids. Part II: Suspensions at finite concentration. J. Rheol. 62 (6), 1379–1396.10.1122/1.5024698Google Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. 2001 Normal stresses and free surface deformation in concentrated suspensions of noncolloidal spheres in a viscoelastic fluid. J. Rheol. 45 (5), 1065–1084.10.1122/1.1396356Google Scholar