Article contents
Shear dispersion of multispecies electrolyte solutions in the channel domain
Published online by Cambridge University Press: 06 September 2023
Abstract
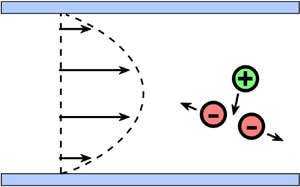
In multispecies electrolyte solutions, even in the absence of an external electric field, differences in ion diffusivities induce an electric potential and generate additional fluxes for each species. This electro-diffusion process is well-described by the advection Nernst–Planck equation. This study aims to analyse the long-time behaviour of the governing equation under electroneutrality and zero current conditions, and to investigate how the diffusion-induced electric potential and shear flow enhance the effective diffusion coefficients of each species in channel domains. The exact solutions of the effective equation with certain special parameters, as well as the asymptotic analyses for ions with large diffusivity discrepancies, are presented. Furthermore, there are several interesting properties of the effective equation. First, it is a generalization of the Taylor dispersion, with a nonlinear diffusion tensor replacing the scalar diffusion coefficient. Second, the effective equation exhibits a scaling relation, revealing that the system with a weak flow is equivalent to the system with a strong flow under scaled physical parameters. Third, in the case of injecting an electrolyte solution into a channel containing well-mixed buffer solutions or electrolyte solutions with the same ion species, if the concentration of the injected solution is lower than that of the pre-existing solution, then the effective equation simplifies to a multi-dimensional diffusion equation. However, when introducing the electrolyte solution into a channel filled with deionized water, the ion–electric interaction results in several phenomena not present in the advection–diffusion equation, including upstream migration of some species, spontaneous separation of ions, and non-monotonic dependence of the effective diffusivity on Péclet numbers. Finally, the dependence of effective diffusivity on concentration and ion diffusivity suggests a method to infer the concentration ratio of each component and ion diffusivity by measuring the effective diffusivity.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 7
- Cited by


