Article contents
Scale-dependent alignment, tumbling and stretching of slender rods in isotropic turbulence
Published online by Cambridge University Press: 07 December 2018
Abstract
We examine the dynamics of slender, rigid rods in direct numerical simulation of isotropic turbulence. The focus is on the statistics of three quantities and how they vary as rod length increases from the dissipation range to the inertial range. These quantities are (i) the steady-state rod alignment with respect to the perceived velocity gradients in the surrounding flow, (ii) the rate of rod reorientation (tumbling) and (iii) the rate at which the rod end points move apart (stretching). Under the approximations of slender-body theory, the rod inertia is neglected and rods are modelled as passive particles in the flow that do not affect the fluid velocity field. We find that the average rod alignment changes qualitatively as rod length increases from the dissipation range to the inertial range. While rods in the dissipation range align most strongly with fluid vorticity, rods in the inertial range align most strongly with the most extensional eigenvector of the perceived strain-rate tensor. For rods in the inertial range, we find that the variance of rod stretching and the variance of rod tumbling both scale as 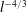 $l^{-4/3}$, where
$l^{-4/3}$, where 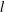 $l$ is the rod length. However, when rod dynamics are compared to two-point fluid velocity statistics (structure functions), we see non-monotonic behaviour in the variance of rod tumbling due to the influence of small-scale fluid motions. Additionally, we find that the skewness of rod stretching does not show scale invariance in the inertial range, in contrast to the skewness of longitudinal fluid velocity increments as predicted by Kolmogorov’s
$l$ is the rod length. However, when rod dynamics are compared to two-point fluid velocity statistics (structure functions), we see non-monotonic behaviour in the variance of rod tumbling due to the influence of small-scale fluid motions. Additionally, we find that the skewness of rod stretching does not show scale invariance in the inertial range, in contrast to the skewness of longitudinal fluid velocity increments as predicted by Kolmogorov’s 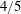 $4/5$ law. Finally, we examine the power-law scaling exponents of higher-order moments of rod tumbling and rod stretching for rods with lengths in the inertial range and find that they show anomalous scaling. We compare these scaling exponents to predictions from Kolmogorov’s refined similarity hypotheses.
$4/5$ law. Finally, we examine the power-law scaling exponents of higher-order moments of rod tumbling and rod stretching for rods with lengths in the inertial range and find that they show anomalous scaling. We compare these scaling exponents to predictions from Kolmogorov’s refined similarity hypotheses.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
Footnotes
Present address: Department of Civil and Environmental Engineering, University of Wisconsin-Madison, Madison, WI 53706, USA; Email address for correspondence: npujara@wisc.edu
References
- 16
- Cited by

