Article contents
Relaxation and coalescence of two equal-sized viscous drops in a quiescent matrix
Published online by Cambridge University Press: 25 January 2012
Abstract
Head-on collisions of two equal-sized viscous drops in a biaxial extensional flow were simulated using the boundary integral method in the Stokes flow limit, for capillary numbers of the order of 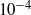 –
–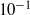 , typical of flow-induced coalescence experiments. At a certain point in time, during the drainage process, the flow was abruptly stopped and the time-dependent dynamics of drop deformation (relaxation) was followed to discern whether the pair of drops would eventually coalesce. The concept of coalescence probability was used to study the evolution of probable collisions. The polymeric system of polybutadiene (PBd) drops undergoing head-on collisions in a polydimethylsiloxane (PDMS) matrix, previously well-characterized both experimentally and numerically by Yoon et al. (Phys. Fluid, vol. 19, 2007, 102102), in which both fluids were Newtonian under the experimental conditions, was used as our reference. Film shapes, velocity profiles and pressure distributions were studied for initially parabolic or dimpled thin film shapes. It was shown that micrometre-sized drops undergoing relaxation can coalesce in the capillary number range studied, which also included cases of hindered coalescence and cases in which the flow interaction time for the collision was smaller than the drainage time; thus, this phenomenon could influence the final drop size distribution of blends. Further, these findings could be of interest in interpreting stop–strain experiments, in the case of a sudden change in flow conditions and in population balance studies of drops in blends.
, typical of flow-induced coalescence experiments. At a certain point in time, during the drainage process, the flow was abruptly stopped and the time-dependent dynamics of drop deformation (relaxation) was followed to discern whether the pair of drops would eventually coalesce. The concept of coalescence probability was used to study the evolution of probable collisions. The polymeric system of polybutadiene (PBd) drops undergoing head-on collisions in a polydimethylsiloxane (PDMS) matrix, previously well-characterized both experimentally and numerically by Yoon et al. (Phys. Fluid, vol. 19, 2007, 102102), in which both fluids were Newtonian under the experimental conditions, was used as our reference. Film shapes, velocity profiles and pressure distributions were studied for initially parabolic or dimpled thin film shapes. It was shown that micrometre-sized drops undergoing relaxation can coalesce in the capillary number range studied, which also included cases of hindered coalescence and cases in which the flow interaction time for the collision was smaller than the drainage time; thus, this phenomenon could influence the final drop size distribution of blends. Further, these findings could be of interest in interpreting stop–strain experiments, in the case of a sudden change in flow conditions and in population balance studies of drops in blends.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 10
- Cited by

