Article contents
Regimes of wettability-dependent and wettability-independent bouncing of a drop on a solid surface
Published online by Cambridge University Press: 11 December 2020
Abstract
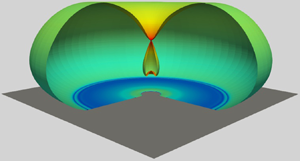
Tiny drops of millimetre size are known to bounce on a solid surface if the surface is superhydrophobic. Recent experiments show that bouncing can occur even on hydrophilic surfaces under conditions where the drop is supported on a thin cushion of gas preventing it from making contact with the surface. We present a detailed insight into this observation by simulating bouncing dynamics of a drop on a flat solid surface using axisymmetric direct numerical simulations. The dynamics of drop motion is governed by three important dimensionless parameters, namely, Reynolds number,  $Re$, Weber number,
$Re$, Weber number,  $We$, and capillary number,
$We$, and capillary number,  $Ca_g$. We generate a phase diagram in the
$Ca_g$. We generate a phase diagram in the  $We\text {--}Re$ plane separating the wettability-independent (non-contact bouncing) and wettability-dependent (contact bouncing) regions. We show that
$We\text {--}Re$ plane separating the wettability-independent (non-contact bouncing) and wettability-dependent (contact bouncing) regions. We show that  $We=2.14$ is the optimum value of Weber number which can support a gas cushion for the widest range of Reynolds numbers. The phase diagram is further divided into five sub-regions based on the shape of the drop and the gas film beneath it. The simulations can reproduce experimentally reported gas films of
$We=2.14$ is the optimum value of Weber number which can support a gas cushion for the widest range of Reynolds numbers. The phase diagram is further divided into five sub-regions based on the shape of the drop and the gas film beneath it. The simulations can reproduce experimentally reported gas films of  ${\sim }1\ \mathrm {\mu }\textrm {m}$ with excellent agreement spatially and temporally. Simulations also reproduce well-known scaling laws for a variety of parameters characterising the gas film. New scaling laws for the radial extent of the gas film as well as time taken for impact are derived. For higher Weber and Reynolds numbers, a bouncing drop captures a gas bubble inside it consistent with simple experiments carried out for water drops bouncing on superhydrophobic surfaces.
${\sim }1\ \mathrm {\mu }\textrm {m}$ with excellent agreement spatially and temporally. Simulations also reproduce well-known scaling laws for a variety of parameters characterising the gas film. New scaling laws for the radial extent of the gas film as well as time taken for impact are derived. For higher Weber and Reynolds numbers, a bouncing drop captures a gas bubble inside it consistent with simple experiments carried out for water drops bouncing on superhydrophobic surfaces.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 16
- Cited by


