Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Scheeler, Martin W.
Kleckner, Dustin
Proment, Davide
Kindlmann, Gordon L.
and
Irvine, William T. M.
2014.
Helicity conservation by flow across scales in reconnecting vortex links and knots.
Proceedings of the National Academy of Sciences,
Vol. 111,
Issue. 43,
p.
15350.
Zuccher, Simone
and
Ricca, Renzo L.
2015.
Helicity conservation under quantum reconnection of vortex rings.
Physical Review E,
Vol. 92,
Issue. 6,
Moffatt, H. K.
2015.
Magnetic relaxation and the Taylor conjecture.
Journal of Plasma Physics,
Vol. 81,
Issue. 6,
Kurgansky, M. V.
2015.
A simple hydrodynamic model of tornado-like vortices.
Izvestiya, Atmospheric and Oceanic Physics,
Vol. 51,
Issue. 3,
p.
292.
Brenner, Michael P.
Hormoz, Sahand
and
Pumir, Alain
2016.
Potential singularity mechanism for the Euler equations.
Physical Review Fluids,
Vol. 1,
Issue. 8,
Clark di Leoni, P.
Mininni, P. D.
and
Brachet, M. E.
2016.
Helicity, topology, and Kelvin waves in reconnecting quantum knots.
Physical Review A,
Vol. 94,
Issue. 4,
Chian, Abraham C.-L.
Feng, Heng Q.
Hu, Qiang
Loew, Murray H.
Miranda, Rodrigo A.
Muñoz, Pablo R.
Sibeck, David G.
and
Wu, De J.
2016.
GENESIS OF INTERPLANETARY INTERMITTENT TURBULENCE: A CASE STUDY OF ROPE–ROPE MAGNETIC RECONNECTION.
The Astrophysical Journal,
Vol. 832,
Issue. 2,
p.
179.
Yoshida, Z.
and
Morrison, P. J.
2017.
Epi-Two-Dimensional Fluid Flow: A New Topological Paradigm for Dimensionality.
Physical Review Letters,
Vol. 119,
Issue. 24,
Scheeler, Martin W.
van Rees, Wim M.
Kedia, Hridesh
Kleckner, Dustin
and
Irvine, William T. M.
2017.
Complete measurement of helicity and its dynamics in vortex tubes.
Science,
Vol. 357,
Issue. 6350,
p.
487.
Villois, Alberto
Proment, Davide
and
Krstulovic, Giorgio
2017.
Universal and nonuniversal aspects of vortex reconnections in superfluids.
Physical Review Fluids,
Vol. 2,
Issue. 4,
Kimura, Yoshifumi
and
Moffatt, H. K.
2018.
A tent model of vortex reconnection under Biot–Savart evolution.
Journal of Fluid Mechanics,
Vol. 834,
Issue. ,
Kedia, Hridesh
Kleckner, Dustin
Scheeler, Martin W.
and
Irvine, William T. M.
2018.
Helicity in superfluids: Existence and the classical limit.
Physical Review Fluids,
Vol. 3,
Issue. 10,
Kimura, Y
and
Moffatt, H K
2018.
Scaling properties towards vortex reconnection under Biot–Savart evolution.
Fluid Dynamics Research,
Vol. 50,
Issue. 1,
p.
011409.
Moffatt, Keith
and
Dormy, Emmanuel
2019.
Self-Exciting Fluid Dynamos.
Yao, Jie
and
Hussain, Fazle
2020.
On singularity formation via viscous vortex reconnection.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
Yao, Jie
and
Hussain, Fazle
2020.
A physical model of turbulence cascade via vortex reconnection sequence and avalanche.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Nguyen, F.
Laval, J.-P.
and
Dubrulle, B.
2020.
Characterizing most irregular small-scale structures in turbulence using local Hölder exponents.
Physical Review E,
Vol. 102,
Issue. 6,
Ostilla-Mónico, Rodolfo
McKeown, Ryan
Brenner, Michael P.
Rubinstein, Shmuel M.
and
Pumir, Alain
2021.
Cascades and reconnection in interacting vortex filaments.
Physical Review Fluids,
Vol. 6,
Issue. 7,
Angriman, S.
Cobelli, P. J.
Bourgoin, M.
Huisman, S. G.
Volk, R.
and
Mininni, P. D.
2021.
Broken Mirror Symmetry of Tracer’s Trajectories in Turbulence.
Physical Review Letters,
Vol. 127,
Issue. 25,
Chakraborty, Priyam
Roy, Arnab
and
Chakraborty, Suman
2021.
Topology and transport in generalized helical flows.
Physics of Fluids,
Vol. 33,
Issue. 11,
 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\nu $ in the limit
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\nu $ in the limit 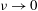 $\nu \rightarrow 0$ . When the vortices are skew to each other, they are annihilated under this action over a local extent that increases exponentially in the stretching direction, with clear evidence of reconnection on the same strain time-scale. The initial helicity associated with the skewed geometry is eliminated during the process of reconnection. The model applies equally to the reconnection of weak magnetic flux tubes under the action of a strain field, when Lorentz forces are negligible.
$\nu \rightarrow 0$ . When the vortices are skew to each other, they are annihilated under this action over a local extent that increases exponentially in the stretching direction, with clear evidence of reconnection on the same strain time-scale. The initial helicity associated with the skewed geometry is eliminated during the process of reconnection. The model applies equally to the reconnection of weak magnetic flux tubes under the action of a strain field, when Lorentz forces are negligible.
