Article contents
Receptivity of a supersonic boundary layer to solid particulates
Published online by Cambridge University Press: 18 November 2013
Abstract
Laminar–turbulent transition in the boundary layer at supersonic speeds can be initiated by small solid particles present in the free stream. Particulates interacting with the boundary-layer flow generate unstable wavepackets related to Tollmien–Schlichting (TS) waves. The latter grow downstream and ultimately break down to turbulent spots. This scenario of TS-dominated transition is modelled using the Mack amplitude method. A theoretical model describing the receptivity mechanism is developed to predict the initial spectrum of TS waves. With these initial conditions the downstream growth of TS instability is calculated using the linear stability theory. The transition onset is associated with the point where the disturbance amplitude reaches a threshold value. As an example, calculations are carried out for a 14° half-angle sharp wedge flying in the standard atmosphere at altitude 20 km, Mach number 4 and zero angle of attack. It is shown that spherical particles of radius from 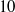 $10$ to
$10$ to 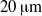 $20~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and density
$20~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and density 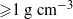 ${\geqslant }1~\mathrm{g} ~{\mathrm{cm} }^{- 3} $ can cause transition onset corresponding to the amplification factor
${\geqslant }1~\mathrm{g} ~{\mathrm{cm} }^{- 3} $ can cause transition onset corresponding to the amplification factor  $N= 9{\unicode{x2013}} 10$ , which is in the empirical range of flight data. This indicates that atmospheric particulates may be a major source of TS-dominated transition on aerodynamically smooth surfaces at supersonic speeds. The receptivity model provides a foundation for further treatments of different cases associated with transition in dusty environments. It can also be used for predictions of particle-induced transition at subsonic and hypersonic speeds.
$N= 9{\unicode{x2013}} 10$ , which is in the empirical range of flight data. This indicates that atmospheric particulates may be a major source of TS-dominated transition on aerodynamically smooth surfaces at supersonic speeds. The receptivity model provides a foundation for further treatments of different cases associated with transition in dusty environments. It can also be used for predictions of particle-induced transition at subsonic and hypersonic speeds.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 59
- Cited by

