Article contents
Plume flows in porous media driven by horizontal differential heating
Published online by Cambridge University Press: 06 March 2012
Abstract
In this paper we describe flow through a porous medium in a two-dimensional rectangular cavity driven by differential heating of the impermeable lower surface. The upper surface is held at constant pressure and at a constant temperature equal to the minimum temperature of the lower surface, while the sidewalls are impermeable and thermally insulated. Numerical results for general values of the Darcy–Rayleigh number 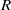 and the cavity aspect ratio
and the cavity aspect ratio 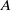 are compared with theoretical predictions for the small Darcy–Rayleigh number limit
are compared with theoretical predictions for the small Darcy–Rayleigh number limit 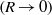 where the temperature field is conduction-dominated, and with a boundary-layer theory for the large Darcy–Rayleigh number limit
where the temperature field is conduction-dominated, and with a boundary-layer theory for the large Darcy–Rayleigh number limit 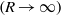 where convection is significant. In the latter case a horizontal boundary layer near the lower surface conveys fluid to the hot end of the cavity where it rises to the upper surface in a narrow plume. Predictions are made of the vertical heat transfer through the cavity.
where convection is significant. In the latter case a horizontal boundary layer near the lower surface conveys fluid to the hot end of the cavity where it rises to the upper surface in a narrow plume. Predictions are made of the vertical heat transfer through the cavity.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 1
- Cited by

