Hostname: page-component-5b777bbd6c-4n89n Total loading time: 0 Render date: 2025-06-24T05:33:43.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Pattern formation on an ice surface

Published online by Cambridge University Press:  23 June 2025

Zhihua Wang Open the ORCID record for Zhihua Wang [Opens in a new window] ,
Kwing-So Choi Open the ORCID record for Kwing-So Choi [Opens in a new window] ,
Shuguang Li Open the ORCID record for Shuguang Li [Opens in a new window] ,
Chao Sun Open the ORCID record for Chao Sun [Opens in a new window]  and
Xuerui Mao Open the ORCID record for Xuerui Mao [Opens in a new window]
Zhihua Wang
Affiliation:
Faculty of Engineering, University of Nottingham, Nottingham NG7 2RD, UK
Kwing-So Choi
Affiliation:
Faculty of Engineering, University of Nottingham, Nottingham NG7 2RD, UK
Shuguang Li
Affiliation:
Faculty of Engineering, University of Nottingham, Nottingham NG7 2RD, UK
Chao Sun
Affiliation:
Department of Engineering Mechanics, School of Aerospace Engineering, Tsinghua University, Beijing 100084, PR China
Xuerui Mao*
Affiliation:
Beijing Institute of Technology (Zhuhai), Zhuhai 519087, PR China School of Interdisciplinary Science, Beijing Institute of Technology, Beijing 100081, PR China
*
Corresponding author: Xuerui Mao, maoxuerui@sina.com
Get access Rights & Permissions [Opens in a new window]

Abstract

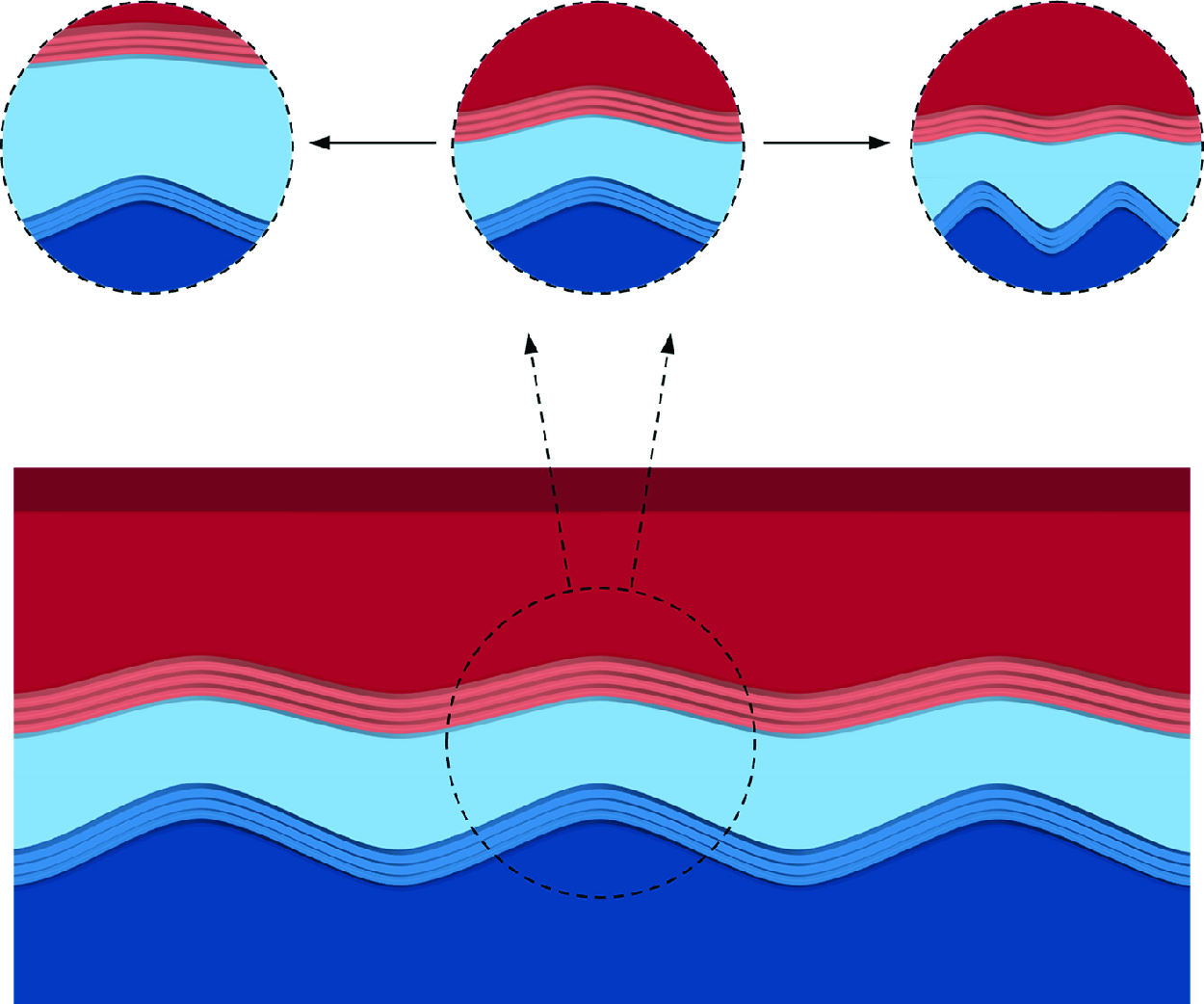
A linear stability model based on a phase-field method is established to study the formation of ripples on the ice surface. The pattern on horizontal ice surfaces, e.g. glaciers and frozen lakes, is found to be originating from a gravity-driven instability by studying ice–water–air flows with a range of water and ice thicknesses. Contrary to gravity, surface tension and viscosity act to suppress the instability. The results demonstrate that a larger value of either water thickness or ice thickness corresponds to a longer dominant wavelength of the pattern, and a favourable wavelength of 90 mm is predicted, in agreement with observations from nature. Furthermore, the profiles of the most unstable perturbations are found to be with two peaks at the ice–water and water–air interfaces whose ratio decreases exponentially with the water thickness and wavenumber.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Nonlinear Dynamical Systems: Pattern formation Phase change: Morphological instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1013 , 25 June 2025 , A35
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adkins, R., Shelton, E.M., Renoult, M.-C., Carles, P. & Rosenblatt, C. 2017 Interface coupling and growth rate measurements in multilayer Rayleigh–Taylor instabilities. Phys. Rev. Fluids 2 (6), 062001.10.1103/PhysRevFluids.2.062001CrossRefGoogle Scholar
Allen, S.M. & Cahn, J.W. 1979 A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta. Metall. 27 (6), 1085–1095.10.1016/0001-6160(79)90196-2CrossRefGoogle Scholar
Aslangil, D. & Wong, M.L. 2023 Investigation of strong isothermal stratification effects on multi-mode compressible Rayleigh–Taylor instability. Phys. Fluids 35 (8), 084116.10.1063/5.0164504CrossRefGoogle Scholar
Badillo, A. 2012 Quantitative phase-field modeling for boiling phenomena. Phys. Rev. E 86 (4), 041603.10.1103/PhysRevE.86.041603CrossRefGoogle ScholarPubMed
Blackburn, J. & She, Y. 2019 A comprehensive public-domain river ice process model and its application to a complex natural river. Cold Reg. Sci. Technol. 163, 44–58.10.1016/j.coldregions.2019.04.010CrossRefGoogle Scholar
Boettinger, W.J., Warren, J.A., Beckermann, C. & Karma, A. 2002 Phase-field simulation of solidification. Annu. Rev. Mater. Sci. 32 (1), 163–194.10.1146/annurev.matsci.32.101901.155803CrossRefGoogle Scholar
Boomkamp, P.A.M., Boersma, B.J., Miesen, R.H.M. & Beijnon, G.V. 1997 A Chebyshev collocation method for solving two-phase flow stability problems. J. Comput. Phys. 132 (2), 191–200.10.1006/jcph.1996.5571CrossRefGoogle Scholar
Bushuk, M., Holland, D.M., Stanton, T.P., Stern, A. & Gray, C. 2019 Ice scallops: a laboratory investigation of the ice–water interface. J. Fluid Mech. 873, 942–976.10.1017/jfm.2019.398CrossRefGoogle ScholarPubMed
Cahn, J.W. & Hilliard, J.E. 1958 Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (2), 258–267.10.1063/1.1744102CrossRefGoogle Scholar
Camporeale, C. & Ridolfi, L. 2012 a Hydrodynamic-driven stability analysis of morphological patterns on stalactites and implications for cave paleoflow reconstructions. Phys. Rev. Lett. 108 (23), 238501.10.1103/PhysRevLett.108.238501CrossRefGoogle ScholarPubMed
Camporeale, C. & Ridolfi, L. 2012 b Ice ripple formation at large Reynolds numbers. J. Fluid Mech. 694, 225–251.10.1017/jfm.2011.540CrossRefGoogle Scholar
Charru, F., Andreotti, B. & Claudin, P. 2013 Sand ripples and dunes. Annu. Rev. Fluid Mech. 45 (1), 469–493.10.1146/annurev-fluid-011212-140806CrossRefGoogle Scholar
Cheng, T., Liu, S.-G., Liu, X.-Y., Hao, N., Teng, A.-P. & Li, Y.-J. 2014 Effects of density and thickness of interlayer on RT instability of interfaces. Commun. Theor. Phys. 61 (5), 649–653.10.1088/0253-6102/61/5/19CrossRefGoogle Scholar
Dadvand, A., Bagheri, M., Samkhaniani, N., Marschall, H. & Wörner, M. 2021 Advected phase-field method for bounded solution of the Cahn–Hilliard Navier–Stokes equations. Phys. Fluids 33 (5), 053311.10.1063/5.0048614CrossRefGoogle Scholar
Drazin, P.G. 2002 Introduction to Hydrodynamic Stability. Cambridge University Press.10.1017/CBO9780511809064CrossRefGoogle Scholar
Faghri, A. & Zhang, Y. 2006 Transport Phenomena in Multiphase Systems. Elsevier.Google Scholar
Gelfgat, A.Y., Bar-Yoseph, P.Z., Solan, A. & Kowalewski, T.A. 1999 An axisymmetry-breaking instability of axially symmetric natural convection. Intl J. Transport Phenom. 1, 173–190.Google Scholar
Grivet, R., Monier, A., Huerre, A., Josserand, C. & Séon, T. 2022 Contact line catch up by growing ice crystals. Phys. Rev. Lett. 128 (25), 254501.10.1103/PhysRevLett.128.254501CrossRefGoogle ScholarPubMed
Guo, H.-Y., Wang, L.-F., Ye, W.-H., Wu, J.-F. & Zhang, W.-Y. 2017 Rayleigh–Taylor instability of multi-fluid layers in cylindrical geometry. Chinese Phys. B 26 (12), 125202.10.1088/1674-1056/26/12/125202CrossRefGoogle Scholar
Hillig, W.B. 1998 Measurement of interfacial free energy for ice/water system. J. Cryst. Growth 183 (3), 463–468.10.1016/S0022-0248(97)00411-9CrossRefGoogle Scholar
Jacobs, J.W. & Dalziel, S.B. 2005 Rayleigh–Taylor instability in complex stratifications. J. Fluid Mech. 542, 251–279.10.1017/S0022112005006336CrossRefGoogle Scholar
Kaser, G., Cogley, J.G., Dyurgerov, M.B., Meier, M.F. & Ohmura, A. 2006 Mass balance of glaciers and ice caps: consensus estimates for 1961–2004. Geophys. Res. Lett. 33 (19), L19501.10.1029/2006GL027511CrossRefGoogle Scholar
Kim, J. 2012 Phase-field models for multi-component fluid flows. Commun. Comput. Phys. 12 (3), 613–661.10.4208/cicp.301110.040811aCrossRefGoogle Scholar
Leppäranta, M. 2010 Modelling the formation and decay of lake ice. The Impact of Climate Change on European Lakes. 63–83.10.1007/978-90-481-2945-4_5CrossRefGoogle Scholar
Li, K., Zhuo, G., Zhang, Y., Liu, C., Chen, W. & Lü, C. 2022 Hypergravitational Rayleigh–Taylor instability in solids. Extreme Mech. Lett. 55, 101809.10.1016/j.eml.2022.101809CrossRefGoogle Scholar
Liu, C. & Shen, J. 2003 A phase field model for the mixture of two incompressible fluids and its approximation by a Fourier-spectral method. Physica D 179 (3–4), 211–228.10.1016/S0167-2789(03)00030-7CrossRefGoogle Scholar
Lundbek Hansen, J., van Hecke, M., Haaning, A., Ellegaard, C., Haste Andersen, K., Bohr, T. & Sams, T. 2001 Instabilities in sand ripples. Nature 410 (6826), 324–324.10.1038/35066631CrossRefGoogle Scholar
Makkonen, L. 1988 A model of icicle growth. J. Glaciol. 34 (116), 64–70.10.3189/S0022143000009072CrossRefGoogle Scholar
Matsuoka, C. 2020 Nonlinear dynamics of double-layer unstable interfaces with non-uniform velocity shear. Phys. Fluids 32 (10), 102109.10.1063/5.0023558CrossRefGoogle Scholar
McDonald, G.D., Méndez Harper, J., Ojha, L., Corlies, P., Dufek, J., Ewing, R.C. & Kerber, L. 2022 Aeolian sediment transport on Io from lava–frost interactions. Nat. Commun. 13 (1), 2076.10.1038/s41467-022-29682-xCrossRefGoogle ScholarPubMed
Mikaelian, K.O. 1982 Rayleigh–Taylor instabilities in stratified fluids. Phys. Rev. A 26 (4), 2140–2158.10.1103/PhysRevA.26.2140CrossRefGoogle Scholar
Mirjalili, S., Ivey, C.B. & Mani, A. 2019 Comparison between the diffuse interface and volume of fluid methods for simulating two-phase flows. Intl J. Multiphase Flow 116, 221–238.10.1016/j.ijmultiphaseflow.2019.04.019CrossRefGoogle Scholar
Murata, K.-I., Nagashima, K. & Sazaki, G. 2019 How do ice crystals grow inside quasiliquid layers? Phys. Rev. Lett. 122 (2), 026102.10.1103/PhysRevLett.122.026102CrossRefGoogle ScholarPubMed
Ogawa, N. & Furukawa, Y. 2002 Surface instability of icicles. Phys. Rev. E 66 (4), 041202.10.1103/PhysRevE.66.041202CrossRefGoogle ScholarPubMed
Parhi, S. & Nath, G. 1991 A sufficient criterion for Rayleigh–Taylor instability of incompressible viscous three-layer flow. Intl J. Engng Sci. 29 (11), 1439–1450.10.1016/0020-7225(91)90049-9CrossRefGoogle Scholar
Piriz, A.R., Sun, Y.B. & Tahir, N.A. 2013 Rayleigh–Taylor stability boundary at solid–liquid interfaces. Phys. Rev. E 88 (2), 023026.10.1103/PhysRevE.88.023026CrossRefGoogle ScholarPubMed
Popović, P., Cael, B B., Silber, M. & Abbot, D.S. 2018 Simple rules govern the patterns of Arctic sea ice melt ponds. Phys. Rev. Lett. 120 (14), 148701.10.1103/PhysRevLett.120.148701CrossRefGoogle ScholarPubMed
Rayleigh, L. 1882 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 1 (1), 170–177.Google Scholar
Reitzle, M., Ruberto, S., Stierle, R., Gross, J., Janzen, T. & Weigand, B. 2019 Direct numerical simulation of sublimating ice particles. Intl J. Therm. Sci. 145, 105953.10.1016/j.ijthermalsci.2019.05.009CrossRefGoogle Scholar
Rignot, E. & Kanagaratnam, P. 2006 Changes in the velocity structure of the Greenland ice sheet. Science 311 (5763), 986–990.10.1126/science.1121381CrossRefGoogle ScholarPubMed
Sabouri-Ghomi, M., Provatas, N. & Grant, M. 2001 Solidification of a supercooled liquid in a narrow channel. Phys. Rev. Lett. 86 (22), 5084–5087.10.1103/PhysRevLett.86.5084CrossRefGoogle Scholar
Sato, K. & Koshimura, S. 2023 A filtering approach for the conservative Allen–Cahn equation solved by the lattice Boltzmann method and a numerical study of the interface thickness. Intl J. Multiphase Flow 167, 104554.10.1016/j.ijmultiphaseflow.2023.104554CrossRefGoogle Scholar
Sengupta, A., Ulloa, H.N. & Joshi, B. 2023 Multi-layer Rayleigh–Taylor instability: consequences for naturally occurring stratified mixing layers. Phys. Fluids 35 (10), 102110.10.1063/5.0170319CrossRefGoogle Scholar
Shen, J. 2011 Modeling and numerical approximation of two-phase incompressible flows by a phase-field approach. In Multiscale Modeling and Analysis for Materials Simulation (ed. W. Bao & Q. Du), pp. 147–195. World Scientific.10.1142/9789814360906_0003CrossRefGoogle Scholar
Shen, J. & Yang, X. 2009 An efficient moving mesh spectral method for the phase-field model of two-phase flows. J. Comput. Phys. 228 (8), 2978–2992.10.1016/j.jcp.2009.01.009CrossRefGoogle Scholar
Straka, P., Meerschaert, M.M., McGough, R.J. & Zhou, Y. 2013 Fractional wave equations with attenuation. Fract. Calc. Appl. Anal. 16 (1), 262–272.10.2478/s13540-013-0016-9CrossRefGoogle ScholarPubMed
Taylor, G.I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A: Math. Phys. Sci. 201(1065), 192–196.Google Scholar
Terrones, G. 2005 Fastest growing linear Rayleigh–Taylor modes at solid/fluid and solid/solid interfaces. Phys. Rev. E 71 (3), 036306.10.1103/PhysRevE.71.036306CrossRefGoogle ScholarPubMed
Ueno, K. 2003 Pattern formation in crystal growth under parabolic shear flow. Phys. Rev. E 68 (2), 021603.10.1103/PhysRevE.68.021603CrossRefGoogle ScholarPubMed
Ueno, K. 2004 Pattern formation in crystal growth under parabolic shear flow. II. Phys. Rev. E 69 (5), 051604.10.1103/PhysRevE.69.051604CrossRefGoogle Scholar
Ueno, K. 2007 Characteristics of the wavelength of ripples on icicles. Phys. Fluids 19 (9), 093602.10.1063/1.2775484CrossRefGoogle Scholar
Ueno, K. & Farzaneh, M. 2011 Linear stability analysis of ice growth under supercooled water film driven by a laminar airflow. Phys. Fluids 23 (4), 042103.10.1063/1.3575605CrossRefGoogle Scholar
Ueno, K., Farzaneh, M., Yamaguchi, S. & Tsuji, H. 2009 Numerical and experimental verification of a theoretical model of ripple formation in ice growth under supercooled water film flow. Fluid Dyn. Res. 42 (2), 025508.10.1088/0169-5983/42/2/025508CrossRefGoogle Scholar
Wang, Z., Calzavarini, E., Sun, C. & Toschi, F. 2021 How the growth of ice depends on the fluid dynamics underneath. Proc. Natl Acad. Sci. USA 118 (10), e2012870118.10.1073/pnas.2012870118CrossRefGoogle ScholarPubMed
Wang, Z., Zhang, W., Mao, X., Choi, K.-S. & Li, S. 2024 A consistent phase-field model for three-phase flows with cylindrical/spherical interfaces. J. Comput. Phys. 516, 113297.10.1016/j.jcp.2024.113297CrossRefGoogle Scholar
Watkins, R.H., Bassis, J.N. & Thouless, M.D. 2021 Roughness of ice shelves is correlated with basal melt rates. Geophys. Res. Lett. 48 (21), e2021GL094743.10.1029/2021GL094743CrossRefGoogle Scholar
Weady, S., Tong, J., Zidovska, A. & Ristroph, L. 2022 Anomalous convective flows carve pinnacles and scallops in melting ice. Phys. Rev. Lett. 128 (4), 044502.10.1103/PhysRevLett.128.044502CrossRefGoogle ScholarPubMed
Zhang, H., Zhang, X., He, F., Lv, C. & Hao, P. 2022 a How micropatterns affect the anti-icing performance of superhydrophobic surfaces. Intl J. Heat Mass Transfer 195, 123196.10.1016/j.ijheatmasstransfer.2022.123196CrossRefGoogle Scholar
Zhang, W., Shahmardi, A., Choi, K.-S., Tammisola, O., Brandt, L. & Mao, X. 2022 b A phase-field method for three-phase flows with icing. J. Comput. Phys. 458, 111104.10.1016/j.jcp.2022.111104CrossRefGoogle Scholar
Zwally, H.J., Giovinetto, M.B., Li, J., Cornejo, H.G., Beckley, M.A., Brenner, A.C., Saba, J.L. & Yi, D. 2005 Mass changes of the Greenland and Antarctic ice sheets and shelves and contributions to sea-level rise: 1992–2002. J. Glaciol. 51 (175), 509–527.10.3189/172756505781829007CrossRefGoogle Scholar